프로그램 명: coci_hipercijevi
제한시간: 1 초
[요약]
은하계에서 가장 빠른 이동 수단은 하이퍼튜브를 이용하는 것이다.
각 하이퍼튜브는 K 개의 정거장을 서로 서로 연결한다.
1 번 정거장에서 N 번 정거장을 가기 위한 최소 정거장 수를 구하시오.
예를 들어 입력이 다음과 같다면
9 3 5 // 9(N) 개의 정거장 , 각 하이퍼튜브에 연결된 정거장 수 3(K) 개 , 5 개의 하이퍼튜브
1 2 3 // 1 번 하이퍼튜브에 연결된 정거장
1 4 5 // 2 번 ....
3 6 7
5 6 7
6 8 9
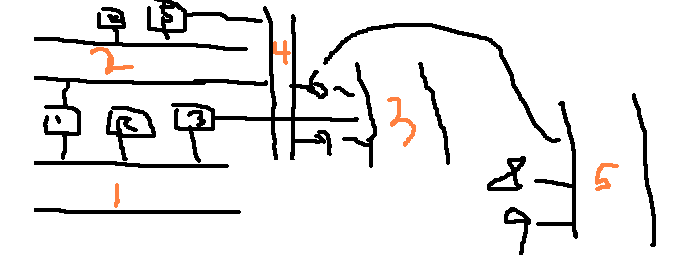
가는 길이 존재하지 않는다면 -1 을 출력한다.
In a galaxy far, far away, the fastest method of transportation is using hypertubes. Each hypertube
directly connects K stations with each other. What is the minimum number of stations that we need to
pass through in order to get from station 1 to station N?
입력
-
The first line of input contains three positive integers: N (1 ≤ N ≤ 100 000), the number of stations, K
(1 ≤ K ≤ 1 000), the number of stations that any single hypertube directly interconnects, and M (1 ≤ M
≤ 1 000), the number of hypertubes.
-
Each of the following M lines contains the description of a single hypertube: K positive integers, the
labels of stations connected to that hypertube.
출력
The first and only line of output must contain the required minimum number of stations. If it isn't
possible to travel from station 1 to station N, output -1.
입출력 예
input
9 3 5
1 2 3
1 4 5
3 6 7
5 6 7
6 8 9
output
4
input
15 8 4
11 12 8 14 13 6 10 7
1 5 8 12 13 6 2 4
10 15 4 5 9 8 14 12
11 12 14 3 5 6 1 13
output
3
Clarification of the first example: It is possible to travel from station 1 to station 9 using only four
stations in the following ways: 1-3-6-9, or 1-5-6-9.
출처:coci/2012-2013/contest5 4번/6
[질/답]
[제출 현황]
[푼 후(0)]

