프로그램 명: coci_guma
제한시간: 1 초

당신은 나무판을 세로로 N번 잘라서 총 N+1개의 조각이 생겼다. 하지만 당신은 나무판을 가로로 또 잘라야 한다. 이때 k번째 조각은 Ak 등분으로 균등하게 잘라야 한다.

한편, 당신은 최신식 레이저 톱이 있어서 당신이 원하는 나무판들을 한번에 가로로 자를 수 있다. 그런데 이 장비의 원리(철판으로 안 자를 곳을 가리고 레이저 작동)에 따르면 한번에 자를 수 있는 지점들은 모두 같은 가로줄 상에 있어야 한다. 톱을 한 번 작동시킬 때마다 매우 많은 전력을 소모하기 때문에 당신은 톱을 최대한 적게 작동시켜야 한다. 잘라야 하는 나무판의 정보가 주어질 때 톱을 사용하는 횟수의 최솟값을 구하는 프로그램을 작성하여라.

입력 형식

첫 번째 줄에는 나무판을 자른 횟수 N이 주어진다. (1 ≤ N ≤ 100,000) 두 번째 줄부터 N+1개의 줄에는 각 조각의 등분 수 Ak 가 주어진다. (0 ≤ A ≤ 100,000) 전체 데이터의 20%는 N ≤ 100이다.

출력 형식

레이저 톱을 작동시키는 횟수의 최솟값을 출력한다. 
입력 예 1

1
2
5

출력 예 1

5

입력 예 2

2
3
7
14

출력 예 2

15

입력 예 3

9
4
2
4
1
2
2
2
8
2

출력 예 3

7
A factory called Gumi-Gumi is dedicated to making tires. Their carving machine is responsible for carving fillisters into the tire. The tire has N vertical fillisters which divide the rubber into N+1 vertical parts. Horizontal cuts are made on each vertical part so that all parts comprising the vertical part are of equal size. The machine can make fillisters on one or more not necessarily continuous vertical sections in one cut, but it can only cut in a straight line.

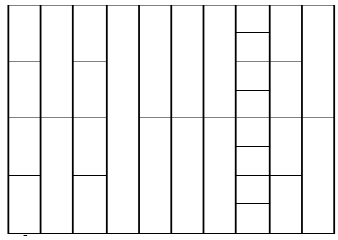
An example of a tire cutting strategy, corresponding to the third sample test. The topmost and the lowest lines represent a full horizontal cut, whereas the first and the last vertical lines are the ends of the tire.

You are given the shape of the tire. Your task is to calculate the minimal possible number of cuts necessary in order to obtain such shape.

INPUT

OUTPUT

The first and only line of output must consist of the minimal number of cuts required.

SCORING

In test cases worth 20% of total points, N will not exceed 100.

SAMPLE TESTS 

input

1
2
5

output

5

input

2
3
7
14

output

15

input

9
4
2
4
1
2
2
2
8
4
2

output

7
Clarification of the first example: On the first day, each table will socialise only with itself so the answer for groups sized 1 is 1. Already on the second day, people sitting at tables 1 and 2 are going to get 5 candies per capita and socialise together, so the answer for a group sized 2 is 2. On the third day, tables 1, 2 and 3 will socialise (because they all have 3 candies per capita). On the sixth day, tables 1, 2, 3 and 4 will socialise (because they now have 1 candy per capita). Finally, on the twelfth day, all tables will socialise together because they will all get zero candy per capita. Clarification of the second example: All tables have the same amount of candy per capita, so a group sized less than 3 will never exist. 
출처:coci/2013-2014/contest4
번역:functionx
[질/답] [제출 현황] [푼 후(0)]
[ 채 점 ] [홈으로]  [뒤 로]