미코는 재미나는 여러가지 일을 했지만 그의 궁금 증은 사라지지 않는다. 그는 공책을 꺼내어서 색을 가진 정사각형을 그리기 시작하다 재미 나는 문제가 생각이 났다.
N 행 N 열을 가진 테이블이 주어질 때 , 각 셀은 검은색 아니면 흰색이다. 수직 , 수평 모서리를 따라 여러 사각형을 만들 때 , 이 때 선택되어진 사각형 셀이 모두 검은색이고 적어도 두 개의 셀을 포함한다면 검은 사각형이라 부르기로 하자.

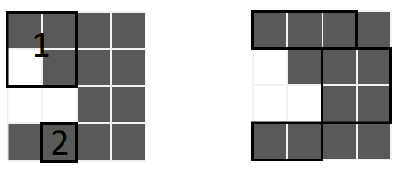
왼쪽 그림의 두개의 사각형은 검은 사각형이 아니다. 그림의 1 번 사각형은 흰 셀을 포함하고 있고 , 2 번 사각형은 한 셀만을 가지고 있다. 오른쪽 사각형들은 모두 검은사각형 이다.
공통의 셀을 포함하지 않은 두 개의 검은 사각형을 선택할 수 있는 조합의 수를 구하는 것이 문제이다. 구한 수가 매우 크기 때문에 이 수를 10 007 로 나눈 나머지를 출력한다.
다음 N 줄당 N 개의 문자가 주어진다. 'C' 는 검은 셀 , 'B' 는 흰 셀이다.
입력 2 CC CC 출력 2 입력 3 CCB CCB CBB 출력 5 입력 5 BCCBB BBCBB BCCBB BBBBB CCBBB 출력 8
출처:coci 2010