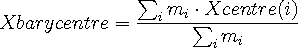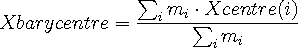프로그램 명: coci_blo(special judge)
제한시간: 1 초
번역 중...
무게 mi 를 가지고 높이가 h 인 N 개의 직사각형이 좌표축에 다음과 같은 형식으로 놓여진다.
-
직사각형은 좌표 축에 평행하다.
-
y 축으로 모든 사각형이 다르고 다음 값을 가진다. 0, h, 2h, 3h, …, (N - 1)h;
-
가장 아래에 있는 직사각형의 왼쪽 좌표는 (-2,0) 이고 오른쪽 좌표는 원점과 일치한다.
직사각형의 X-center 는 아래의 면의 중간 점의 x 값이다
하나 혹은 이상의 X-barycentre 는 그들의 X-center 의 가중치의 평균이다.
즉 다음과 같이 계산된다.
다시 말해 각 직사각형의 무게와 X-center 와 곱해지고 이 곱의 합이 직사각형의 전체 무게로 나누어진다.
직사각형 A 가 다음과 같이 놓여진다면 안정된다.
-
the X-barycentre of rectangles above A has distance of at most 1 from the X-centre of A (i.e. is
contained in the x-interval that covers A).
A 위에 있는 사각형들의 X-barycentre 가 A 의 X-centre 의 부터 많아야 1 의 거리를 가진다면
(즉 A 위의 x-interval 에 포함된다면)
Intuitively, stability of an arrangement can be understood as the precondition for the arrangement to not fall apart.
직관적으로 , 정돈의 안정되었다는 것은 떨어지지 않는 정돈의 사전 조건으로 이해 될 수 있다.
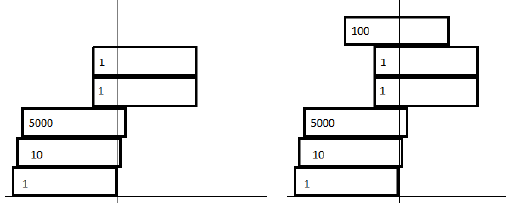
The arrangement in the figure on the left is unstable since the X-barycentre of the top two rectangles falls outside the rectangle underneath (the distance of the X-barycentre to the X-centre of the underlying rectangle is greater than 1).
그림에서 왼쪽의 그림은 불 안정하다. 왜냐하면 위에 있는 두 개의 직사각형이 아래로 떨어진다. ( 왜냐하면 아래에 놓여 있는 사각형의
X-centre
오른쪽 그림은 안정적이다.
모던 직사각형의 무게가 주어질 때 , 안정적이기 위한
가장 큰(가장 오른쪽)의 가능한 x 좌표를 찾는 것이 문제이다.
사각형의 순서를 바꾸는 것은 허용되지 않는다.( 밑에서 위 순으로 사각형이 주어진다)
N rectangles with given masses (mi) and equal lengths (2) and heights (h) are arranged in a Cartesian
plane such that:
-
rectangle edges are parallel to the coordinate axes;
-
the y-coordinates of lower horizontal edges are distinct and assume the following values: 0, h,
2h, 3h, …, (N - 1)h;
-
the lowest rectangle's lower left corner has coordinates (-2, 0), while the lower right corner
coincides with the origin.

The X-centre of a rectangle is the x-coordinate of the midpoint of its lower edge.
The X-barycentre of one or more rectangles is the weighted average of their X-centres. It is computed as
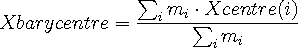
In other words, the mass of each rectangle is multiplied by its X-centre and the sum of these products
is then divided by the total mass of the rectangles.
An arrangement is stable if, for each rectangle A:
-
the X-barycentre of rectangles above A has distance of at most 1 from the X-centre of A (i.e. is
contained in the x-interval that covers A).
Intuitively, stability of an arrangement can be understood as the precondition for the arrangement to
not fall apart. The arrangement in the figure on the left is unstable since the X-barycentre of the top
two rectangles falls outside the rectangle underneath (the distance of the X-barycentre to the X-centre
of the underlying rectangle is greater than 1). The arrangement in the figure on the right is stable.
Given the masses of all rectangles, find the largest (“rightmost”) possible x-coordinate of any
rectangle corner in a stable arrangement. You are not allowed to change the order of rectangles (they
are given from the lowest to the highest one).
입력
The first line of input contains the positive integer N (2 ≤ N ≤ 300 000), the number of rectangles.
Each of the next N lines contains a single positive integer less than 10 000, the mass of a rectangle. The
masses are given in order from the lowest to the highest rectangle.
출력
The first and only line of output must contain the required rightmost x-coordinate. The given result
must be within 0.000001 of the official solution.
입출력 예
입력
2
1
1
출력
1.000000
입력
3
1
1
1
출력
1.500000
입력
3
1
1
9
출력
1.900000
출처:coci 2011-2012 contest5 5/6
[질/답]
[제출 현황]
[푼 후(0)]