Our recycling company is about to process waste that comes in railway wagons. There are N wagons waiting on the incoming railway track, and each wagon contains exactly one type of waste. Waste is processed according to one of a fixed number of settings. For each setting we are given the set of waste types that can be processed with this setting. Sadly, changing the setting is a very time-consuming operation, therefore the company uses one setting a day.

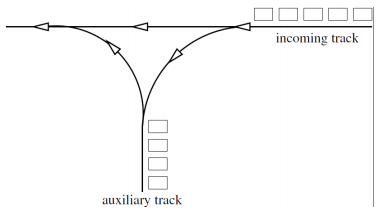
The wagons are to be processed in the order they arrive on the incoming railway track. To speed up recycling, the company has built an auxiliary track as shown on the figure below. This way, if the next wagon contains waste that cannot be processed with the current setting, then it can be moved to the auxiliary track, preceding the wagons that are already there. The next wagon to be processed is the first in row from either the incoming track or the auxiliary track. Mind that no wagon can be moved back from the auxiliary to the incoming track. The company wants to recycle as many wagons of waste as possible within the next three days. At the end of the third day the auxiliary track must be empty

Task

입력

• The first line of the input contains three integers, N (1 ≤ N ≤ 20 000) is the number of wagons, K (1 ≤ K ≤ 1000) is the number of waste types, and S (1 ≤ S ≤ 1000) is the number of settings. Wagons are numbered from 1 to N, waste types are numbered from 1 to K and settings are numbered from 1 to S.
• The next S lines contain the description of the settings. The (i+1)th line of the input contains a space-separated list of integers terminated by a 0, the set of waste types that can be processed with setting i,.
• The last line is a list of N integers describing the wagons: the ith number is the identifier of the type of the waste contained in wagon i. For each type x there is at least one and at most 10 settings that contain waste of that type.

출력

• The first line of the output contains one integer, the maximum number of wagons that can be processed.
• The second line of the output contains three integers separated by space, the setting for the first, the second and the third day. If two days are enough for processing all wagons then the third number must be 0. Similarly, if one day is enough then the second number must also be 0.

If there are multiple solutions, your program should output only one; it does not matter which one.

입출력 예

입력

13 5 4
1 0
4 5 0
5 3 0
2 5 0
4 5 2 5 5 4 1 1 5 4 5 3 3

출력

11
2 1 4 

출처:ceoi 2012