Our engineers have designed a communication network that consists of nodes and unidirectional direct communication channels (links) between some pairs of nodes. We say that a node q is reachable from node p on a path, if there is a sequence of different nodes p1,p2,…,pk with p=p1 and q=pk, such that there is a link that transmits data from pi to pi+1 for every i=1,…,k-1.

This network has a central node r, such that any other node p can be reached from r via a path, and for any pair of nodes p and q there is at most one path on which q can be reached from p. The maintainers plan to improve on the network, but have not yet decided how. One idea they are considering is to reassign the central node, therefore they want to know for each node how many nodes are reachable from it on a path. Another idea is to just decentralize the network, so they also want to know how they could introduce new links so that for any pair of nodes p and q, there is exactly one path on which the node q can be reached from p, and vice versa.

Task

입력

• The first line of the input contains three integers, N (1 ≤ N ≤ 100 000) the number of nodes, M (1 ≤ M ≤ 500 000) the number of links, and r (1 ≤ r ≤ N) the central node. Nodes are numbered from 1 to N.
• The next M lines contain the description of the links. Each line contains two integers p and q separated by space, that corresponds to a link, which can transmit data from p to q.

출력

• The first line of the output contains the solution to Subtask A: N integers separated by space, where the ith number is the number of reachable nodes from node i (including i itself).
• The remaining lines contain the solution for Subtask B: The second line of the output contains one integer K, the minimum number of new links needed to achieve the above property of the network. The next K lines list the new links: each of lines contains two integers u and v separated by space, that corresponds to a new link transmitting data from node u to node v.

입출력 예

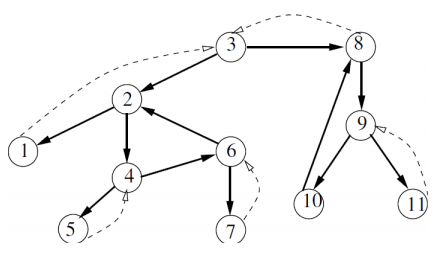
입력

11 12 3
3 2
2 1 
2 4 
4 5 
4 6 
6 2 
6 7
3 8
8 9
9 10
9 11
10 8

출력

1 6 11 6 1 6 1 4 4 4 1
5
1 3
5 4
7 6
11 9
8 3

출처:ceoi 2012