프로그램 명: boi_treemirroring
제한시간: 1 초

Let T be a rooted tree (a connected undirected acylic graph), and let S be a perfect copy of T. Construct a new graph by taking the union of T and S, and merging the corresponding leaf nodes (but never the root). We call such a graph a tree-mirrored graph.

Write a program that determines if an arbitrary undirected connected graph is a tree-mirrored graph

입력

The first line of input contains two integers N and M, the number of vertices and edges of a graph G. The vertices in G are labeled from 1 to N. The following M lines describe the edges. Each such line contains two integers x and y (x =6 y; 1 x; y N), describing one edge. There will be at most one edge between any pair of vertices.

출력

The first and only line of output should contain the string YES if the graph G is a tree-mirrored graph, and NO otherwise.

Constraints

3 N; M 100 000 In test cases worth 60 points, 3 N; M 3 500. In test cases worth 30 points, 3 N; M 300.

입출력 예

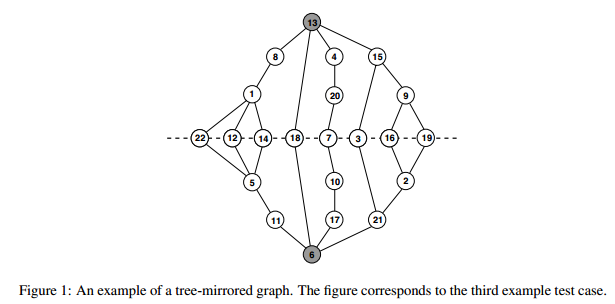
입력

7 7
1 2
2 3
3 4
4 5
5 6
6 7
7 1 

출력

NO

입력

6 6
1 2
2 3
2 4
3 5
4 5
5 6

출력

YES

입력

22 28
13 8
8 1
1 22
1 12
1 14
13 18
13 4
4 20
20 7
13 15
15 3
15 9
9 16
9 19
22 5
12 5
14 5
5 11
11 6
18 6
7 10
10 17
17 6
3 21
21 6
16 2
19 2
2 21

출력

YES

The last example input corresponds to the graph in the figure.

출처:BOI 2011 day2 3/3
[질/답] [제출 현황] [푼 후(0)]
[ 채 점 ] [홈으로]  [뒤 로]