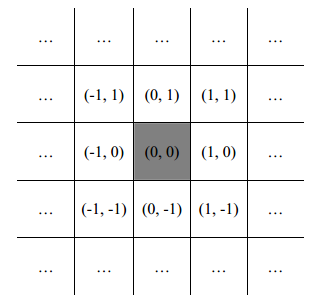
A space station is being built on a planet. The station will employ N persons. They have to live somewhere, and for that, a city will be built around the station. The land surrounding the station is divided into equal-sized square lots, and an apartment building with up to K floors may be built on each lot. Each building shall have exactly one apartment on each floor, and each person shall live in a separate apartment. The lots are assigned coordinates in the form (x, y), where the space station has coordinates (0, 0) and the rest of the lots are numbered as shown below:

As the traffic can only flow on streets between the lots, the distance of the lot (x, y) from the space station is |x| + |y| - 1 units. The cost of building a house is equal to the sum of the costs of each floor. It is known that the cost to build a floor depends on the height of the floor, but not on the location of the building.

The houses to be built will last for 30 years. People living in those houses will go to work in the space station, and to transport them to and from the station during these 30 years will cost T·d per person, where d is the distance of the person’s building from the station.

We can assume that the planet is big enough and the city to be built occupies a small enough portion of the surface that we do not need to consider the curvature of the planet’s surface.

Your task is to write a program that determines the minimal total cost of building the houses and operating the transportation system for the 30 years.

입력

• The first line of the input file contains the integers N (1 ≤ N ≤ 1 000 000 000 000), T (1 ≤ T ≤ 500 000), and K (1 ≤ K ≤ 20 000).
• The following K lines specify the costs of building the apartments on each floor. The (i + 1)-th line contains the integer ci (1 ≤ ci ≤ 2 000 000 000), the cost of building an apartment on the i-th floor (assuming all the i - 1 floors below have already been built).

출력

입출력 예

입력

17 5 4 
100 
107 
114 
121 

출력
   
1778 

출처:boi 2006