2 차원 평면상에 n 개의 점이 주어져 있을 때, 어느 한 점부터 시작하여 모든 점을 한 번만 방문한 다음, 다시 그 점으로 돌아오는 가장 짧은 사이클(closed cycle)을 찾는 문제(이를 판매원 여행 문제(Travel Salesman Problem)이라 한다.)는 잘 알려진 NP-hard 문제로서 다항 시간(Polynomial time)내에 이 문제를 해결하는 알고리즘은 아직 존재 하지 않는다.

그러나, 이 문제를 다음과 같이 제한을 가하여 단순화하면 다항시간에 해결될 수 있음이 알려져 있다.

즉, 가장 왼쪽점부터 시작하여 x-좌표값이 증가하는 순서로 점을 방문하여 가장 오른쪽 점까지 도달한 다음, 다시 그 점부터 가장 왼쪽 점까지 x-좌표값이 감소하는 정렬의 순서대로 방문하는 가장 짧은 사이클을 찾는 것이다. 이러한 사이클을 bitonic Cycle 이라고 부른다.

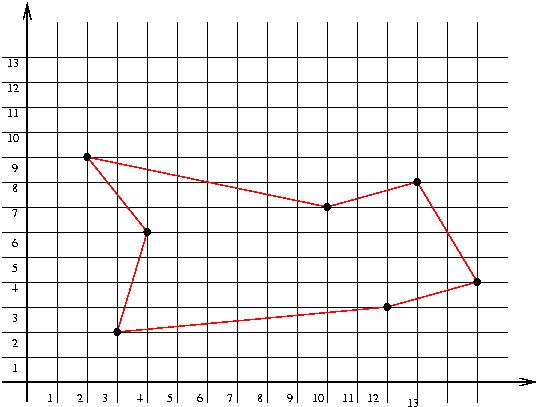
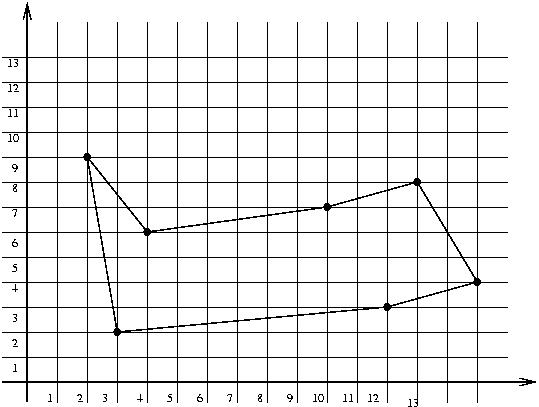
TSP	Bitonic cyle

TSP cycle 는 bitonic cycle 보다 전체길이가 더 짧다.

n 개의 점이 임의의 순서로 주어졌을때 (단, 같은 x-좌표를 갖는 점들이 없다고 가정한다),이의 bitonic cycle 을 다항시간에 구하는 프로그램을 작성하라.

입력형식

• 첫 번째 줄에는 점의 개수 n(1 <= n <= 400)이 주어지고,
• 둘째 줄부터 n 개의 줄에는 각 점의 좌표가 x,y 의 순서로 들어온다. 좌표는 -100000 부터 100000 까지이다.

출력형식

입출력 예

입력

7
13 8
3 2
12 3
2 9
15 4
10 7
4 6

출력

36.61

출처:모름
채점데이터:Conankun(algolab.org)