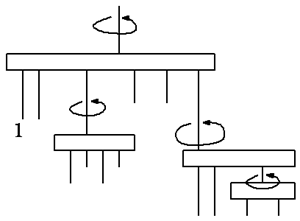
여러 개의 0과 1의 숫자들이 달려있는 모빌이 하나 있다. 모빌은 가로 막대와 그 가로 막대에 0과 1, 혹은 다른 가로 막대가 아래에 차례대로 달려있는 모양으로 구성되어 있다.
예를 들어 하나의 모양을 보면 오른쪽 그림과 같다. 모빌의 균형은 언제나 잘 잡혀있다고 가정하자.

모빌에 바람이 불면 각 가로 막대는 회전을 하게 되는데 그렇게 되면 여러 가지 다른 모양의 모빌을 형성하게 된다.
우리는 모빌의 한 상태에서 하나의 이진수를 만들어 낼 수 있는데, 그 수는 모빌의 현재 상태를 아래와 같은 방법으로 괄호와 0, 1을 사용해서 표현한 것에서, 오른쪽부터 0과 1들을 읽어내면서 만들어지는 수이다.
모빌의 표현은 반드시 여는 괄호로 시작하여 닫는 괄호로 끝난다는 것에 주의하라.
예를 들어, 오른쪽 그림의 모빌의 상태는 아래와 같이 표현된다.
(10(1011)00(10(01)))
위와 같이 표현되는 모빌의 상태에서 만들어지는 이진수는, 괄호들을 제거하면 101011001001 임을 알 수 있다.
만약, 이 상태에서 중간 1011 가로 막대가 회전을 한다면 101101001001이라는 숫자를 얻게 되고, 다시 이 상태에서 가장 상위에 있는 가로 막대가 움직이면 전체의 숫자가 뒤집혀 100100101101이라는 숫자를 얻게 된다.
주어진 모빌로부터 생성이 가능한 이진수를 모빌 이진수라고 말한다.
모빌의 하나의 상태가 주어졌을 때, 그 상태를 변화시키면 매우 다양한 모빌 이진수를 관찰할 수 있는데, 이 문제의 목표는 관찰 가능한 모든 모빌 이진수들 중에서 K 번째로 작은 모빌 이진수를 찾아내는 것이다. 단, 모빌의 서로 다른 형태가 동일한 모빌 이진수를 만들어 내는 경우, 동일한 숫자들은 “하나만” 남기고 나머지는 모두 제거하여야 한다.
예를 들어, 다음과 같은 모빌의 경우,
(0(1(01))1)관찰되는 모빌 이진수는 (크기 순서에 관계없이) 01011, 11010, 10110 등이 있다. 만일 K =3 이라면 모빌 이진수들 중 3번째로 작은 숫자인 01101 을 출력해야 한다.
과정의 일부를 보이면 다음과 같다.
(0((01)1)1) -> 00111 -> 가장 작은 수 (0((10)1)1) -> 01011 -> 2번째로 작은 수 (0(1(01))1) -> 01011 -> 위의 수와 동일 (0(1(10))1) -> 01101 -> 3번째로 작은 수
만일 K 가 관찰 가능한 모든 모빌 이진수의 총 개수보다 많은 경우 (예를 들어, 관찰 가능한 모든 모빌 이진수의 총 개수는 10개인데 K =15로 주어짐), 여러분은 대문자로 NO 를 출력해야 한다.
입력 (0(1(01))1) 3 출력 01101 입력 (0((10)(11))(((01)))1) 5 출력 01101011 입력 (0(1(11))11) 5 출력 NO
출처:koi 2010 중등 2 번