Sam과 여동생 Sara는 n×m 테이블의 모든 셀을 빨간색과 파란색으로 색칠하고자 한다.

이들은 개인적인 믿음 때문에, 테이블의 모든 2 × 2 격자에는 빨간색 셀의 개수가 홀수(즉, 1 혹은 3)가 되기를 원한다.

예를 들어, n×m芼戮遣諮이 조건을 만족하는 색칠의 예가 다음 그림에 있다.

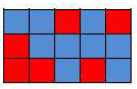
불행히도, 지난 저녁에 누군가가 테이블의 어떤 셀들을 빨간색으로, 또 다른 어떤 셀들은 파란색으로 칠해놓았다.

Sam과 Sara는 모든 n×m 격자에 빨간색 셀의 개수가 홀수가 되도록 테이블의 나머지를 색칠할 수 있는지를 알려고 한다. 만약 가능하다면, 모든×m 격자에 빨간색 셀의 개수가 홀수가 되도록 색칠할 수 있는 방법이 몇 개가 있는지를 알려고 한다.

입력

• 첫 번째 줄에 세 정수 n,m,k가 주어진다. 이들은 각각 테이블의 행의 수, 열의 수, 초기에 색칠되어진 셀의 수이다.

• 다음의 k 개 줄에 색칠된 셀들의 정보가 주어진다.
  이들 k 개 줄의 각 i 번째 줄에는 세 정수 xi,yi,ci 를 포함한다. xi,yi 는 각각 초기에 i -번째 색칠된 셀의 행 번호, 열 번호이고, ci는 이 셀의 색이다. 이 셀이 빨간색으로 칠해져 있으면 ci는 1이고 파란색으로 칠해져 있으면 ci는 0이다. k개의 셀들의 위치는 모두 다르다.

출력

제약 조건

• 초기에 색칠된 각 셀의 행 번호 xi와 열 번호 yi 는 항상 1 <= xi <= n 이고, 1 ≤ yi ≤ m 이다.
• 모든 테스트 케이스에 대하여 2 ≤ n,m ≤10^5 이고 0 ≤ k ≤ 10^5 이다.

입출력 예

입력

3 4 3
2 2 1
1 2 0
2 3 1

출력

8

출처:apio 2011 년 1 번 문제