승현이는 자신이 좋아하는 자연수들로 구성된 수열 $a_{1}, a_{2}, \cdots, a_{n}$을 생각해 냅니다. 그리고, 이 수열에서 서로 다른 세 원소 $a_{i}$, $a_{j}$, $a_{k}$를 선택한 뒤, 이들을 가로, 세로, 높이로 하는 직육면체 모양의 지우개를 만들고 이를 $i-j-k$ 지우개라고 명명하기로 했습니다. 단 승현이는 위로 길쭉한 지우개를 좋아하므로, $a_{i} < a_{j} < a_{k}$를 만족해야 합니다.

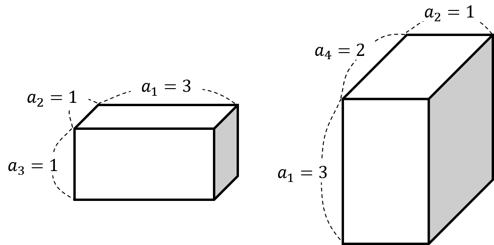
위 그림을 한 번 살펴봅시다. 승현이가 만든 수열을 $a_{1} = 3, a_{2} = 1, a_{3} = 1, a_{4} = 2$라고 둡시다. $1-2-3$ 지우개는 만들 수 없는데, $3 < 1 < 1$은 성립하지 않기 때문입니다. 반면 $2-4-1$ 지우개는 $1 < 2 < 3$이 성립하므로 만들 수 있습니다. 이 수열에서 만들 수 있는 지우개는 $2-4-1$ 지우개와 $3-4-1$ 지우개뿐입니다.
이 때 승현이는 만들 수 있는 모든 지우개들의 부피의 합을 갑자기 알고 싶어집니다. (지우개의 부피는 가로 길이, 세로 길이와 높이의 곱입니다.) 아마 창고에 지우개를 쌓아 놓아야 하니 그렇겠죠? 승현이가 지우개를 보관할 창고를 설계할 수 있도록 우리가 도와줍시다.
첫 번째 줄에 수열의 크기 $n$이 주어집니다.
두 번째 줄에 $a_{1}, a_{2}, \cdots, a_{n}$이 공백을 사이로 두고 차례대로 주어집니다.
첫 번째 줄에 만들 수 있는 지우개들의 부피의 합을 출력합니다. 승현이는 프로그램이 제대로 동작하는 것부터 검증하기를 원하므로, $1,000,000,007$ ($10^{9}+7$)로 나눈 나머지를 출력합시다.
입력 4 3 1 1 2 출력 12
위에 설명한 예제와 같습니다. 만들 수 있는 지우개는 $2-4-1$ 지우개와 $3-4-1$ 지우개뿐이므로, 부피의 합은 $a_{2}a_{4}a_{1} + a_{3}a_{4}a_{1} = 1 \times 2 \times 3 + 1 \times 2 \times 3 = 12$가 됩니다.
출처:geniusainta.com