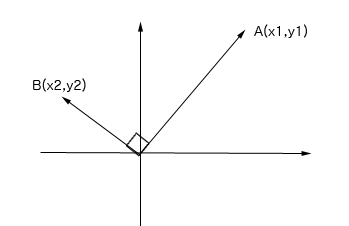
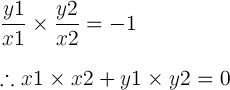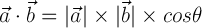이런 화살이 좌표에 다음과 같이 놓여 있다고 생각 해 봅니다.
3 번은 1 번과 방향과 크기가 같고 2,5번은 1 번과 방향만 같습니다.
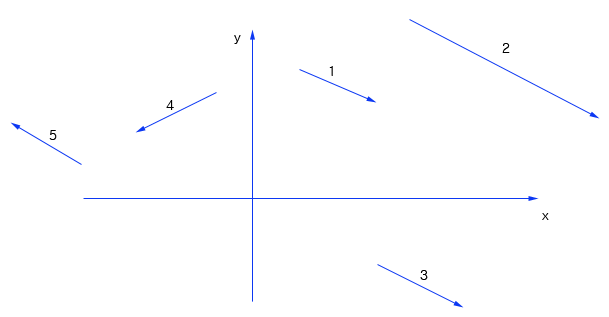
모든 화살을 시점을 원점으로 옮기면 1 , 3 번 같은 화살이되고
1 번 화살을 기준으로 설명을 하자면 3 번은 같은 화살이 되고 2 번과 5 번은 실수배를 하여
만들 수 있습니다.(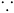
y=ax 꼴의 비례함수)
이렇게 시점을 원점으로 두는 경우(시점이 반드시 원점이 아니어도 관계는 없습니다.) 방향과 크기가 같으면 같은 화살이 됩니다. 이 화살 각각을 vector 라 합니다.
vector 는 방향과 크기가 같으면 같고 크기는 다른 데 방향이 같으면 실수배를 하여 만들 수 있습니다.
이 개념을 3 차원으로 확장해도 같습니다.
1)벡터의 합과 차
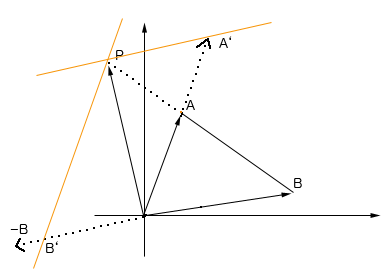
먼저 b' 벡터와 b 벡터는 같은 벡터 입니다. b' 벡터의 시점을 원점으로 놓기 위해서는 종점에서 시점을 각각의 좌표 값으로 빼주면 됩니다. 이 것이 벡터의 뺄셈입니다.
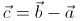
다시 덧셈으로 돌아와서 a 벡터와 b' 의 덧셈은 a 벡터와 b 벡터의 덧셈으로 생각 후 각 좌표 값을 더하면 두 벡터를 평행 사변형으로 만든 후의 시점에서 대각선의 끝점이 됩니다.
그러니 벡터 a 와 벡터 b' 의 덧셈으로 생각하면 꼬리잇기로 b' 의 종점이 합이 됩니다.
2)두 벡터로 다른 벡터를 표현하기
3)어떤 점이 선분 위의 점 인가?
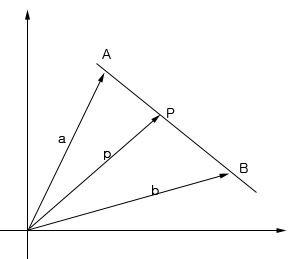
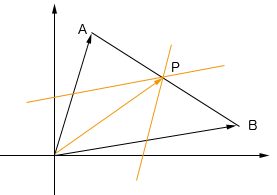
A,P,B 가 일직선 상에 있는 점에 있다. 벡터를 이용해서 이를 어떻게 알수 있을까?
벡터 AP 는 AB 와 방향은 같고 크기가 다릅니다. 즉 AP 벡터에 적당한 실수배를 가하면 AB 벡터를 만들 수 있습니다.
이 식이 벡터에서 매우 중요한 식 입니다.시점을 원점으로 옮긴 벡터로 나타내면
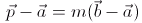
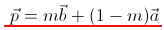
일직선 상에 있기 위한 조건은 벡터 b 의 계수 m 과 벡터 a 의 계수 1-m 으로 계수의 합이 1 이면 일직선 상에 있다라고 할수 있습니다.
이 식을 조금 더 음미 해 볼 필요가 있습니다.
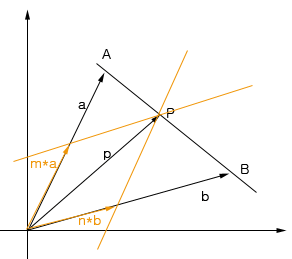
P 점이 AB 선상에 있기 위해서는 벡터 a 를 적당히 줄인 m 값과 벡터 b 를 적당히 줄인 n 값의 합이 1 이다 라는 것 입니다.
그러면 일직선 상에 있는 경우 선분 AB 에 있는지 바깥 쪽 에 있는지를 알수 어떻게 알수 있을까요?
이는 m,n 값을 조사해 보면 알수 있습니다.
먼저 선분 상의 점인지 선분 밖의 점인지를 알아 보도록 하겠습니다.
4)어떤 점이 삼각형 내부의 점인가? 평행사변형 내부의 점인가?
또한 점이 주어질 때 이 점이 삼각형 OAB 안에 있는지 아니면 OA,OB 를 변으로하는 평행 사변형 안에 있는지를 어떻게 알수 있을까요?
