BFS(큐 이용)로 최단거리 구하기

각 정점간 이동하는데 비용이 일정한 경우 queue 를 이용해서 최단 거리를 구할 수 있다.

차례:
    개념
    구현 
    시간 복잡도

1. 개념

각 간선을 이동하는데 비용이 일정한 경우 만약 1 이 든다고 생각 하면 정점 A 를 시작 정점으로 모든 정점으로 가는 데 필요한 최소 비용를 생각해보자.

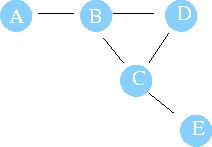
B 까지 가는데는 1
C 까지 가는데는 2
D 까지 가는데는 2 혹 A B C D 로 가는 사람은 없겠죠 ... 당연 A B D
E 는 3 ... A B C E

여러 갈래 돌아가는 길이 있더라도 출발지에서 먹물을 퍼뜨리면 가장 짧은 길로 연결된 지점에 먼저 도착하겠죠.
어떻게 queue 를 이용해서 이 부분을 구하는 가가 핵심인데 이 는 BFS(너비 우선 탐색)를 이용합니다. 이 부분을 모르는 분 들은 queue 파트가 선행되어야 함.

2. 구현

step1.정점에서 갈수 있는  노드 중 이미 방문된 노드를 제외하고 큐에 삽입.

step2.큐에서 데이터를 하나 꺼낸후 goto step1
      이 과정을 큐가 빌때 까지 반복
큐에 삽입되는 노드의 거리는 이 노드에 연결된 이유로 삽입되는 노드이 거리보다 1 많음. 패스를 저장하기 위해서는 전노드의 번호를 저장하면서 구현

(예시 문제) 정점 간의 이동 비용이 1 이라 할 때 1 번 도시에서 모든 도시로의 최단거리 구하는 문제를 생각해 보자.
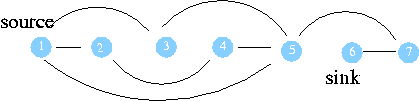
1 번 정점을 큐에 삽입 , 거리는 0
queue
--------------------   
 1 
--------------------
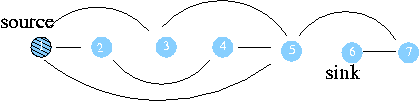
정점 방문유무 1 번도시에서의 최단 거리 아버지 정점

1 방문 0 nil

2

3

4

5

6

7
queue 삭제
삭제된 정점(1)에 연결된 정점이 2 3 4 번 정점 차례로 queue insert
2 3 5 정점의 거리는 아버지 정점의 거리에서 1 을 더함
queue
--------------------   
 2 3 5 
--------------------
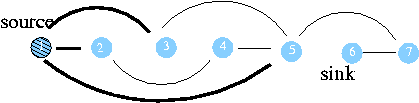
정점 방문유무 1 에서의 거리 아버지 정점

1 방문 0 nil

2 방문 1 1

3 방문 1 1

4

5 방문 1 1

6

7
큐 삭제(2 번 정점). 
2 번 정점에 연결된 정점이 1 4 번 정점. 1 번 정점은 이미 방문되었으므로
4 번 정점 큐 삽입. 4 번 정점의 거리는 2 번 정점의 거리에 1 을 더함(거리는 2)
queue
--------------------   
3 5 4 
--------------------
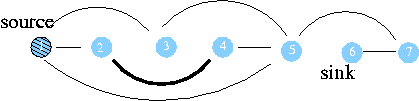
정점 방문유무 1 에서의 거리 아버지 정점

1 방문 0 nil

2 방문 1 1

3 방문 1 1

4 방문 2 2

5 방문 1 1

6

7
3 번에 연결된 정점은 모두 방문되었으므로
5 번 정점에 연결된 정점 중 7 번 정점
7 번 정점의 거리는 5 번 정점의 거리 + 1
queue
--------------------   
4 7
--------------------
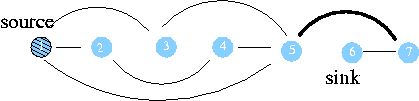
정점 방문유무 1 에서의 거리 아버지 정점

1 방문 0 nil

2 방문 1 1

3 방문 1 1

4 방문 2 2

5 방문 1 1

6

7 방문 2 5
4 번 정점에서 모두 방문
7 번 정점에서는 6 번 정점
queue
--------------------   
6
--------------------
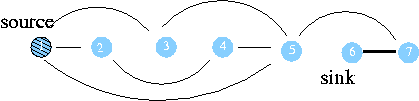
정점 방문유무 1 에서의 거리 아버지 정점

1 방문 0 nil

2 방문 1 1

3 방문 1 1

4 방문 2 2

5 방문 1 1

6 방문 3 7

7 방문 2 5

3. 시간 복잡도

정점(vertex)의 수를 v 라 하면 O(v)

[질/답]

[홈으로] [뒤 로]

[푼 후(0)]