Union-Find 자료구조는 아래 두 작업을 효율적으로 처리할 수 있는 자료구조를 말합니다.
- 두 항목 A, B가 같은 그룹이라는 정보를 새로 추가한다. (Union)
- 주어진 정보만을 가지고 두 항목 A, B가 확실히 같은 그룹에 속해 있는지 구한다. (Find)
예를 들어, 다음 정보가 주어진다고 합시다.
- 멜론과 석류는 같은 바구니에 있습니다.
- 딸기와 수박은 같은 바구니에 있습니다.
- 멜론과 복숭아는 같은 바구니에 있습니다.
과일을 노드라고 할 때, 같은 바구니에 있는 두 과일을 간선으로 이으면 다음과 같은 그래프가 만들어집니다.
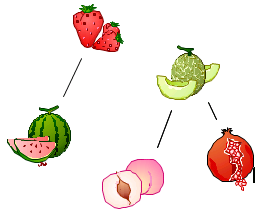
이 때, 간단한 그래프 탐색을 이용해서 [ 딸기, 수박 ] 이 같은 바구니에 있고, [ 복숭아, 멜론, 석류 ] 가 같은 바구니에 있음을 알 수 있습니다. 하지만 여기서 정보가 더 들어오면, 그래프 탐색을 계속 반복해야 하기 때문에 비효율적입니다.
Union-Find 자료구조는 각 노드마다 자신과 같은 그룹에 있는 한 부모 노드를 가리키면서 트리들을 형성하는 방식으로 이루어집니다.
맨 처음에는 모든 노드가 모두 부모 노드가 없습니다. 즉, 루트 노드입니다. 위에서 설명한 과일 바구니 예를 들자면, 아래와 같은 상태가 됩니다.

- 두 항목 A, B가 같은 그룹이라는 정보를 새로 추가한다.
위 명령을 받게 되면, 일단 A, B가 속한 트리의 루트 노드 a, b를 구한 후, b의 부모 노드를 a로 만듭니다. 그러면, A와 a가 같은 그룹이고 B와 b가 같은 그룹이고 a와 b가 같은 그룹이 되므로 자동적으로 A와 B도 같은 그룹이라고 할 수 있습니다. 만약 a와 b가 같다면, 이미 A와 B가 같은 그룹이기 때문에 부모 노드를 설정할 필요가 없습니다.
- 멜론과 석류는 같은 바구니에 있습니다.
- 딸기와 수박은 같은 바구니에 있습니다.
예를 들어, 위 명령들을 수행한 후에는 과일들끼리 연결된 상태가 아래와 같이 변합니다.

- 주어진 정보만을 가지고 두 항목 A, B가 확실히 같은 그룹에 속해 있는지 구한다.
여기서, 위 형태의 명령을 받데 되면, A, B가 속한 트리의 루트 노드 a, b를 구해서 서로 같은지 구합니다. 루트 노드들끼리는 서로 같은 그룹에 있다는 보장이 없기 때문에 a와 b가 다르면 A, B가 같은 그룹이 아닐 수도 있다는 말입니다. 하지만, a와 b가 같으면, A, a, b, B가 모두 같은 그룹에 속해 있다는 것을 알 수 있으므로, A와 B도 같은 그룹에 속해 있습니다.
2개의 명령만을 수행한 상태에서 석류와 복숭아가 확실히 같은 바구니에 있는지 알아봅시다.
-
1) 석류 노드가 속해 있는 트리의 루트 노드는 멜론 노드이다.
-
2) 복숭아 노드가 속해 있는 트리의 루트 노드는 복숭아 노드이다.
-
3) 두 루트 노드가 다르므로 석류와 복숭아가 확실히 같은 바구니에 있는지는 알 수 없다.
한편, 수박과 딸기의 경우, 각 과일이 속해 있는 트리의 루트 노드는 딸기 노드로 일치하므로 수박과 딸기는 확실히 같은 바구니에 있음을 알 수 있습니다.
노드의 수가 N이고 정보의 수가 M이라면, 트리를 구현하면서, 최악의 경우에 노드의 최대 레벨이 N이 될 수 있으므로, 최악의 경우 시간복잡도는 O(MN)이 됩니다.


