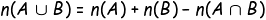
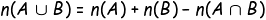
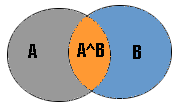
그림에서 세 구역으로 이루어져 있다.
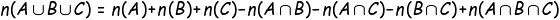 A B C A^B A^C B^C A^B^C
1 1 1 1
1 1 1 1
1 1 1 1
-----------------------
1 1 1 2 2 2 3
A B C D A^B A^C A^D B^C B^D C^D
4 개 인 경우
A B C A^B A^C B^C A^B^C
1 1 1 1
1 1 1 1
1 1 1 1
-----------------------
1 1 1 2 2 2 3
A B C D A^B A^C A^D B^C B^D C^D
4 개 인 경우
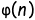 라 하자.
라 하자.
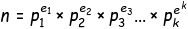
1 - n 사이의 n 과 서로 소인 개수는
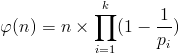
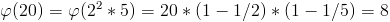
a , p 가 서로 소이고 , p 가 소수이면
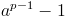 는 p 의 배수이다. 즉
는 p 의 배수이다. 즉 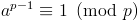
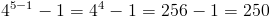 은 5 의 배수이다.
은 5 의 배수이다.
1 , 2 , 3 , .... , p-1 에 p 와 서로 소인 수 a 를 곱하면
1*a , 2*a , 3*a , ... ,(p-1)*a 를 p 로 나누면 나머지가 1 , 2 , ... , p-1 이 된다.
1 , 2 , 3 , 4 , 5 , 6
1*6 , 2*6 , 3 *6 , 4 *6 , 5*6 , 6*6
7로 나눈나머지: 6 , 5 , 4 , 3 , 2 , 1
1 , 2 , 3 , 4 , 5 , 6
1*8 , 2*8 , 3 *8 , 4 *8 , 5*8 , 6*8
7로 나눈나머지: 1 , 2 , 3 , 4 , 5 , 6
7 로 나눈 나머지 1 에서 6 까지가 나온다.
proof)
만약 p 미만의 수 n, m이 있을 때, (n < m) n*a 와 m*a 를 p로 나눈 나머지가 같다고 하자. 즉 두 수의 차인 (m-n)*a는 p의 배수이다. 서로소인 두 수 a, p의 최소공배수는 ap이므로 m-n은 p의 배수이어야 한다. 이 때 m은 최소 n+p인데, n+p >= p일 수밖에 없으므로 모순. 즉 a부터 (p-1)*a 중 mod p가 서로 같은 쌍은 존재하지 않는다. 즉 1부터 p-1까지의 모든 나머지가 나와야 한다. (0이 나올리는 없겠죠이제 페르마 정리를 정리하면 ,
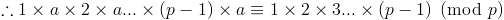
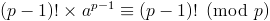
(p-1)! 은 p 와 서로 소이므로 (p-1)! 로 양변을 나누면 a^(p-1) = 1 (mod p)
출처: