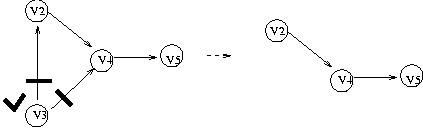AOV network

차례:
-AOV network
-위상 정렬
-방법
-구현 

(1) AOV network

그림은 스타크래프트에서 건물을 짓는 순서 입니다.

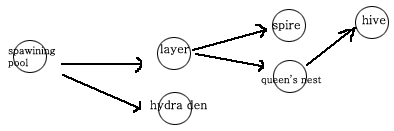
먼저 layer 부터 올릴수는 없죠..... spawning pool 을 짓고 나서 layer 을 올려야 합니다.(아시죠^^)

그러면 건물을 짓기 위한 순서는 어떻게 되나요? ... 여러가지가 있습니다.

몇 가지를 나열해 보면

• 스포닝 풀 -> 덴 -> 레어 -> 스파이어 -> 퀸즈 네스트 -> 하이브
• 스포닝 풀 -> 레어 -> 스파이어-> 퀸즈 네스트 -> 하이브 -> 덴
• ...

동그라미(정점,vertex)가 작업을 나타내고 , 화살표(간선,edge)가 작업의 순서를 나타낸다.

이런 류의 그래프를 AOV(Activity On Vertex) network 라 합니다.

(2) 위상 정렬

AOV 네트워크에서 주된 관심은 일의 순서를 정하는 것입니다.

크기 순이아니고 먼저 해야 할 일 순서이지만 이것도 일종의 정렬이라고 말할 수 있습니다.

이 정렬을 위상 정렬(topological sorting)이라고 합니다.

그래프에서 위상 정렬을 하는 방법은 위에서 보았듯이 여러가지가 존재할 수도 있고 , 존재 하지 않을 수도 있습니다.

그러면 언제 존재하지 않을까요?

(3) 방법

• 진입차수(indegree)가 0 (이 정점보다 앞선 작업이 없다는 것)인 정점을 선택 후
• 이 정점 에서 나가는 진출 차수를 모두 없앤 후
• 다시 진입차수가 0 인 정점을 선택하는 과정을 반복.

이 과정에서 진입 차수가 0 인 정점이 없다면 이는 위상 정렬을 할수가 없으며 이러한 그래프는 AOV 네트워크가 될 수 없습니다. 가만 생각해보면 이러한 그래프는 사이클이 발생하는 그래프라는 것을 알수 있습니다.

예를 들어 다음 그래프를 위상 소트하는 과정을 살펴 봅시다.

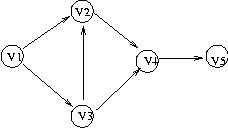
1. 정점 중에 진입차수(indegree)가 없는 정점이 1 번 정점이므로 , 1 번정점을 선택후 1 번 정점에서 나가는 진출차수를 모두 제거

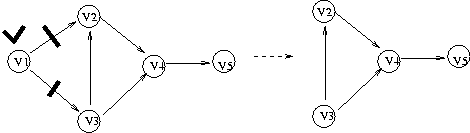
2. 남은 정점 중에 진입차수가 없는 정점이 3 번 정점, 3 번 정점에서 나가는 진출 차수를 모두 제거

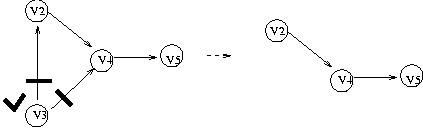
3. 남은 정점 중에 진입차수가 없는 정점이 2 번 정점, 2 번 정점에서 나가는 진출 차수를 모두 제거

4. 남은 정점 중 진입차수가 없는 정점이 4 번 정점, 4 번 정점에서 나가는 진출 차수를 모두 제거

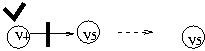
위상소트(topological sort)순서: 1 3 2 4 5

다음 그래프를 위상 소트하면 어떻게 될까요?

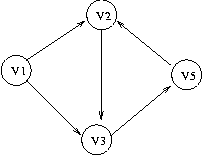
사이클이 존재하는 그래프는 AOV 네트워크가 될 수 없고, 위상정렬을 행할 수도 없습니다.

(4) 구현

• dfs 로 구현한 자료(ppt)
  http://www.cs.princeton.edu/courses/archive/fall06/cos226/demo/demo-topological.ppt

• 세가지 방식으로 설명한 캐나다 맥길 대학 자료(pdf)
  http://cgm.cs.mcgill.ca/~msuder/courses/360/lectures/topological-sort/topological-sort.pdf

출처:dovelet