stack

차례: 
      스택 동작 이해하기
      스택 구현
      overflow ,underflow
      관련 문제 프로그밍 하기
      infix,postfix 표현
      관련 문제 프로그밍 하기

1.스택 동작 이해

stack 구조는 한 쪽끝은 막혀 있고 한 쪽 끝은 뚫려 있는 구조이다.

한쪽 끝이 막혀 있는 구조이므로 막히지 않은 쪽에서 자료의 삽입과 삭제가 발생한다. 일상생활에서 스택구조를 보이는 것은 택시의 동전꼽이,책을 쌓을때 등등의 구조에서 볼수 있고 , 프로그래밍시 내부적으로 함수 call 과 리턴시 사용된다. Last InFirstOout

2.스택 구현

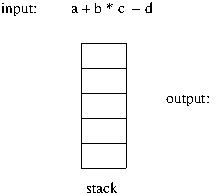
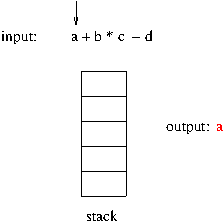
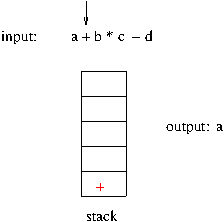
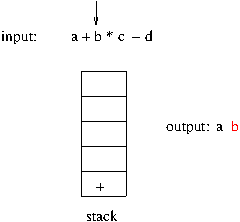
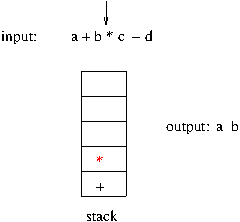
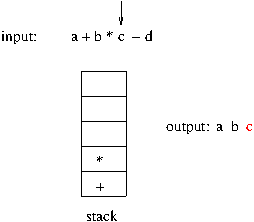
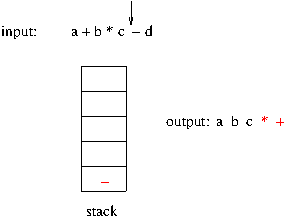
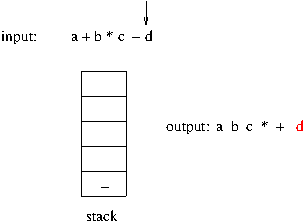
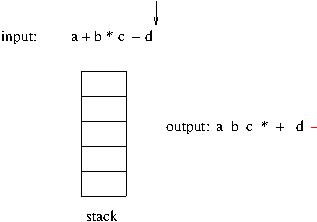
  1. 스택을 구현할 자료 구조는 배열
  2. stack 에서 사용하는 동작 insert ,delete 동작
위 애플릿 구조를 기본으로 설명하면 ,
int stack[6];

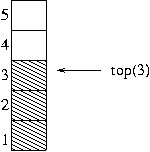
아래 그림은 3 개의 데이터가 미리 스택에 삽입된 상태이다. 스택구조에서는 한쪽 끝의 제일 위에서 삽입과 삭제가 발생하므로 제일 끝을 가르키는 변수가 존재하고 이를 보통 top 이란 변수명으로 사용한다.

(1) 삽입(push)

4 번째 위치에 데이터를 삽입하면 되므로 , top 변수를 하나 증가후 새로은 데이터를 삽입. 

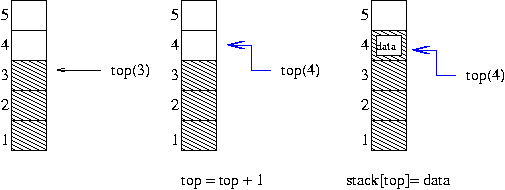top=top+1;
stack[top]=data;

(2)삭제(pop)

3 번째 데이터를 임시변수로 top 변수를 1 감소 하면 되므로 

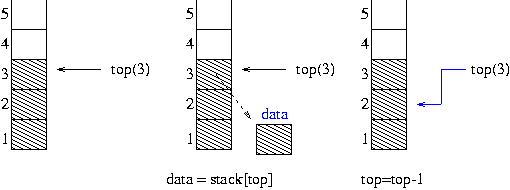data=stack[top]; // stack top 에 있는 자료를  data 로
top=top-1;

3.overflow ,underflow

예외 사항을 생각한다. 삽입시 데이터를 넣을 공간이 있나, 삭제시에는 가져올 자료가 있나를 검사.

위의스택에서는 top 값이 5 이면 데이터를 더 이상 넣을 구간이 없는 경우이고 , top 값이 0 이면 빼내올 데이터가 없는 경우이다.

(1) push 동작 

if (top >=5){
   printf("넣을 공간이 없습니다.");
   exit(1);//강제 종료
}
top=top+1;
stack[top]=top;

(2) pop 동작 

if (top <=0) {
   printf("빈 스택입니다.");
   exit(1);
}
data=stack[top];
top=top-1;

4.관련 문제 프로그래밍 하기

5.infix,prefix,postfix 에 대한 설명

(1)infix,prefix,postfix 란?

중위(infix) 표기
데이터사이에 연산자가 오는 표기법 , 현재 우리가 사용하는 표기
예를 들어, a + b
전위(prefix) 표기
연산자가 데이터앞에 오는 표기법
+ab
후위(postfix) 표기
연산자가 데이터뒤에 오는 표기법
ab+

(2) 문제 제기

a + b *c 란 연산을 생각해 봅니다. 이를 계산하기 위해 한 문자(token)씩 입력을 받습니다.

이렇듯 Infix 표기법은 컴퓨터가 계산하기에는 적당하지 않은 표기법입니다. 이는 prefix 와 postfix 표기법으로 해결할 수 있습니다. (여기에서는 postfix 위주로 설명을 하겠습니다)

infix 를 postfix 로 변경할 때도 stack 을 , postfix 표현의 계산에서도 stack 을 사용합니다.

(3) infix 수식을 postfix 로 바꾸기

1) 괄호 사용
연산자 우선 순위를 적용하여 수식에 괄호를 친 후 왼쪽에서 오른쪽으로 오면서 연산자를 만다면 왼쪽에 있는 가장 가까운 괄호로 옮겨 주면 됩니다. 
(예1) a + b * c 이면 

( a + ( b * c ) )  
          |
          --->
    |
    ----------->

결과:abc*+

(예2) a  +  b * c - d 

괄호를 칩니다.

( a +  ( b * c ) - d ) 

연산자를 옮깁니다.

( ( a +  ( b * c  )  )  - d ) 
                        |
                        ---->
             |
             ---->
      |
      --------------->

결과: abc *+d-

(예3) 괄호가 있는 식 (a + b ) * ( c - d ) 
            
( ( a + b ) * ( c - d ) )
                  |
                  --->
             |
             ----------->
      |
      ---->

결과:ab+cd-*
2) stack 사용
이 괄호 방법은 stack 을 이용해서 구현할 수 있습니다.

높은 연산 우선 순위가 나와야 하므로

  • 오퍼랜드는 그대로 패스
  • 현재 연산자보다 우선순위가 높으면 push
  • 아니면 pop 동작이 이루어지면 됩니다.

      1. step1

      2. step2

      3. step3

      4. step4

      5. step5

      6. step6

      7. step7

      8. step8

      ▒ 괄호가 있는 수식은 어떻해 할까요?

(4) postfix 수식 계산하기

  1. 한 문자씩 입력을 받아서 push
  2. 연산자를 만나면
    • a = pop();
    • b = pop();
    • push (b 연산자 a)
  3. goto 1

6.관련 문제 프로그래밍 하기

[홈으로]  [뒤 로]
[푼 후(0)]