신장 트리란?(spanning tree)

차례.

-신장트리란?
-최소비용 신장트리
-구현 방법(kruskal,prime)

1. 신장 트리(spanning tree)란?

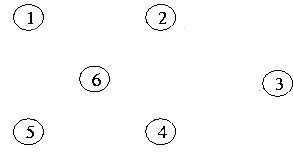
그래프에서

1. 모든 정점을 포함하고 ,
2. 정점간 서로 연결되면서 사이클이 존재하지 않는 그래프 ( 이 조건은 트리 조건 입니다 )

즉 모든 정점을 모두 포함하는 트리를 신장 트리라 합니다.

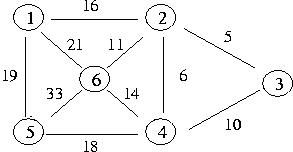
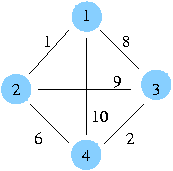
아래 그래프의 신장트리는 존재 할까요? 한다면 몇개가 있을까요?

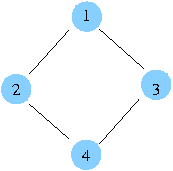
4 가지가 존재하겠죠.

---

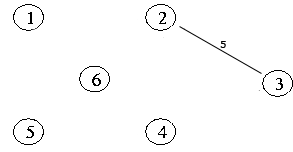
여기에서 간선에 값(cost)을 한 번 부여해 보겠습니다.

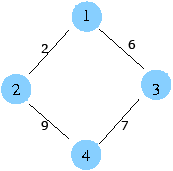
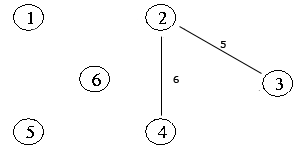
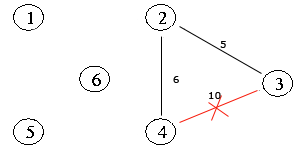
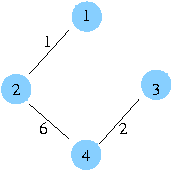
이 경우에 4 개의 신장 트리 중 값의 합이 최소인 신장트리가 있겠죠. 이 신장트리가 최소 비용 신장 트리 입니다.

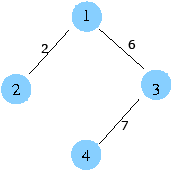
최소 비용은 15 입니다.

2. 최소비용 신장트리(minimal cost spanning tree) 구하는 방법

주어진 그래프에서 최소비용 신장트리를 구하면 ? 그 때의 최소비용은?

이 정도만 하더라도 눈으로 구하는 것이 쉽지가 않습니다. 이 를 구하는 방법으로 널리 알려진 알고리즘으로 Kruskal , prim 방법이 있습니다. 눈으로 구하신 후 두 방법을 사용해서 구한 답이 맞는지 확인 해 보세요.

3. 방법과 구현

두가지 모두 그리디 메소드를 이용합니다. 직관의 힘이 필요합니다.

1) Kruscal 방법

알고리즘

1. 간선중 비용이 적은 순으로 소트
2. 가장 적은 비용이 드는 간선부터 차례대로 추가
3. 추가중 사이클이 존재하는 간선은 제외
4. 모든 정점이 연결될 때 까지 2 - 3 과정을 반복

위에서 든 예로 모든 정점을 포함 해야 하므로 그림과 같이 준비 합니다. 목표는 이 정점들이 사이클을 발생하지 않으면서 모두 연결되어야 합니다.

cost 가 작은 간선 부터 하나씩 연결 합니다.

• 2 , 3 번 정점의 간선 5 를 선택

  

• 2 , 4 번 정점의 간선 6 을 선택

  

• 3 , 4 번 정점의 간선 10 을 선택하면 사이클이 발생하므로 10 을 버림

  

• 2 , 6 번 정점의 11 을 선택
• ...

이 과정을 모든 정점이 연결할 때 까지 반복

구현... union and find 를 이용... 시간 복잡도: O(e loge)

2) Prim 방법

kruskal 방법과 달리 정점을 하나씩 추가. 정정의 수가 n 개이면 n-1 번의 반복이 필요.

알고리즘

1. 임의의 정점을 선택
2. 이 정점에서 다른 정점으로 갈수 있는 최소 비용의 정점을 선택
   이 정점은 제외
3. 이 정점에서 다른 정점으로 가는 비용과 기존의 비용과 비교후 더 작은 비용이 있으면 갱신
4. step4. 2-3 번 과정을 n(정점의수)-1 번 반복

왼쪽 그래프에서 오른쪽의 최소비용 신장트리를 prim 방법으로 구하여 봅니다.

최소비용 신장트리
------------------>








step 1. 임의의 정점(1,2,3,4 중 하나)에서 시작... 3 번 정점에서 시작한다고 하면 





정점



방문유무



아버지 정점



패스크기








1



x



3



8









2



x



3



9





 



3



o



x



0










4



x



3



2







step 2. 방문되지 않는 노드중 패스가 최소인 정점을 선택... 이 간선은 최소비용 스패트 트리의 간선이 됨.(그리디)
        이 정점에 연결된 방문되지 않은 정점 중 패스의 크기가 작은 것이 있으면 갱신
        이 경우 2 번 정점으로 가는 기존의 패스가 9 이고 , 4 에서 2 로 가는 정점이 6 이므로 갱신.








정점



방문유무



아버지 정점



패스크기








1



x



3



8









2



x



3



9









3



o



x



0










4



o



3



2












정점



방문유무



아버지 정점



패스크기








1



x



3



8









2



x



4



6









3



o



x



0










4



o



3



2








step 3. 이 과정을 노드수가 4 개이므로 3 번 반복....