1) 문제의 핵심
bubble 공기방울을 뜻한다. 물 속에서 공기 방울이 있으면 위로 올라오는 경험이 목욕탕에서 있죠 :-)
이 물방은 위로 위로 해서 물 밖으로 나게게 됩니다.
데이터에서 공기방울은 가장 큰데이터가 되어서 가장 뒤로 놓이게 된다고 해서 이런 이름이 붙었는 것 같습니다.
버블소트에서는 인접한 두 원소를 비교해서 두 데이터 중 앞 데이터가 크면 뒤 데이터와 순서를
바꾸면서, 한 판 훌터면서 가장 큰 데이터를 뒤로 보내는 소트 방법이다.
이 과정을 반복하는 방법이 버블소트이다.
2)구현
배열 ia[] 에 아래와 같은 데이터가 있다고 하자.
6 2 9 8 3 4 7
ia[j]의 뒤 원소는 ia[j+1] 이므로, 두 개의 인접한 원소를
비교해서 앞원소가 크면 앞 과 뒤 원소를 교환하면 된다.
if( ia[j] > ia[j+1){
tmp = ia[j];
ia[i] = ia[j+1];
ia[j+1] = tmp;
}
변수 j 값의 범위를 생각해보자.
- 첫 판에는 0 에서 5
- 다음 판에는 0 에서 4
- ...
끝 값이 5 , 4 , 3 , 2 , 1 , 0 로 변하므로 이를 상수로 처리하지는 못하고 , 변수로 처리할
수 있다. 이 변수명을 i 라 하면 소스 는 다음과 같다.
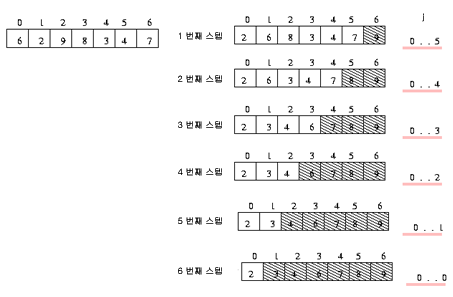
3) 개선된 bubble sort
위 그림 세째 판에서 네째 판으로 넘어올 때 한 번의 자리바꿈도 일어나지 않는다.
이는 세째 판에서 이미 소트가 끝난 상태라는 것이다.
이를 구현하기 위하여 임시 변수(여기에서는 flag) 를 사용하여 해결한다.
for(i = n - 2 ; i >= 0 ; i--){
flag = 0;
for(j = 0;j <= i ; j++)
if (ia[j] > ia[j+1]){
flag = 1;
tmp = ia[j];
ia[j] = ia[j+1];
ia[j+1] = tmp;
}
if (flag==0) break;
}
(작은문제1) 아래와 같은 데이터가 배열 ia[] 에 있다고 할 때 , 이 수 중 가장 작은
데이터의 위치를 찾는 프로그램은?
데이터가 아래와 같을 경우 2 번째 데이터의 위치인 4 를 출력 해야 한다.

(풀이) 0 번째 데이터를 가장 작은 데이터위치로 둔 후 첫 번째부터 끝까지
비교하면서 작은데이터의 위치보다 더 작은 데이터가 존재하면 작은 데이터의
위치를 변경하는 방법.
min_index=0;
for(j=1;j<=6;j++){
if ( ia[min_index] > ia[j]) min_index=j;
(작은문제2) 배열 중에 가장 작은 데이터를 찾아서 그 데이터와 0 번째 데이터를
교환하는 프로그램을 작성.
(풀이) 가장 작은 데이터의 위치를 찾는 루틴은 보기 1 에서 구했으므로 , 이 위치와
0 번째 위치를 교환하는 루틴만 구하면 된다.
min_index=0;
for(j=1;j<=6;j++){
if ( ia[min_index] > ia[j]) min_index=j;
tmp=ia[0];
ia[0]=ia[min_index];
ia[min_index]=tmp;
결과로서 가장 작은 데이터가 0 번째의 위치로 이동한다.

(작은문제3) 아래와 같이 배열ia[] 에 1 , 2, ... ,6 까지의 데이터 중 가장
작은 데이터의 위치를 찾는 프로그램은?

(풀이) 보기 1 에서 처음 min_index 변수에 1 을 두고 j 는 2 부터 6 까지 반복하면
된다.
min_index=1;
for(j=2;j<=6;j++){
if ( ia[min_index] > ia[j]) min_index=j;
이 정렬 방법에 대해서 정리하면 , 기본 개념은 가장 작은 데이터를 선택해서
제일 앞의 데이터와 해당 데이터와 교체하는 방법이다.
- 첫 판에는 min_index 가 0 이고 j 는 1 부터 끝 까지
- 다음 판에는 min_index 가 1 이고 j 는 2 부터 끝 까지
- ...
- 다음 판에는 min_index 가 5 이고 j 는 6
for(i=0;i<6;i++){
min_index=i;
for(j=i+1;j<=6;j++)
if (ia[min_index] > ia[j]) min_index=j;
tmp=ia[i];
ia[i]=ia[min_index];
ia[min_index]=tmp;
}
이 방법은 정렬의 효율은 떨어지지만 소스가 조금 더 간단한 방법인데 ,
위에서 본 selecition 정렬은 가장 작은 데이터를 찾아 제일 앞 데이터와 교환하는
방법인데 반하여 , 이 방법은 비교하면서 제일 앞의 데이터와 바로 교환하는 방법이다.
for( i = 0 ; i < 6 ; i++){
for( j = i+1 ; j <= 6 ; j++){
if ( a[i] > a[j] ){
tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
}
}
이미 정렬된 데이터에서 하나의 원소가 새로 추가되는 경우 효율적으로 소트할수 있는
방법이다.
예를 들어, 학생들이 운동장에서 키순으로 줄을 서 있는 경우 한 학생이 늦게 도착해서
제일 뒤에 섰다. 이 학생은 어떻게 하면 가장 빨리 시끄럽지 않게 자기 자리를 찾아 갈수 있을까를 생각해보자.
이 방법은 어떨까? 앞의 학생과 비교해서 자기보다 크면 그 학생과 자리를 바꾸고 , 다시 앞 학생과
비교해서 자기 보다 크면 자리를 바꾸고 , 이 과정을 반복하다 앞 학생이 자기보다
작거나 같으면 이 학생은 자기자리를 찾은 것이다.
이런 동작을 형태를 보이는 정렬이 삽입 정렬이다.
아래와 같은 정렬된 데이터에서 7 을 추가하고자 하는 경우의 예를 들면
2 4 6 8 10
- 7 과 10 을 비교. 7 이 작으므로 10 을 한 칸 뒤로
- 7 과 8 을 비교. 7 이 작으므로 8 을 한 칸 뒤로
- 7 과 6 을 비교. 7 이 크므로 7 을 삽입후 종료
그림으로 나타내면 ,

보기에서 입력되는 데이터가 1 이라면 예외적인 경우가 발생하는데 앞 데이터와 비교해서
작은면 뒤로 이동한다고 했는데 이런 경우에는 모든 데이터가 뒤로 밀리고 마지막에
1 과 비교할 데이터가 없다. 이런 경우의 해결 방법은 두가지가 있는데
하나는 , 제일 앞 위치에 보초(sentinel)를 세우는 경우인데 이런 경우의 보초는
데이터에서 나올수 없는 아주 작은 데이터를 두면 해결 가능하다.
아래 소스에서 ia[0] 번째 위치에 0 을 둔 것이 그 예가 되겠고 ,
#include < stdio.h >
int ia[]={0,2,4,6,8,9,7};
int main()
{
int i,j;
int tmp;
tmp=ia[6];
j=5;
while (tmp < ia[j]){
ia[j+1]=ia[j];
j--;
}
ia[j+1]=tmp;
//출력
//
for(i=1;i<7;i++)
printf("%d ",ia[i]);
}
소스를 간략하게 설명하면 , 데이터는 배열을 1 번째 위치부터 존재하고 , 0 번째 배열에는
나올수 없는 아주 작은 값으로 보초를 세우는 방법이다.
다른하나는 , 비교할 데이터가 남아 있는지를 검사하는 방법이다.
#include < stdio.h >
int ia[]={2,4,6,8,9,7};
int main()
{
int i,j;
int tmp;
tmp = ia[5];
j = 4;
while (j != -1 && tmp < ia[j]){
ia[j+1] = ia[j];
j--;
}
ia[j+1] = tmp;
//출력
for(i = 0;i < 6; i++)
printf("%d ",ia[i]);
}
간략히 설명하면 , 이 경우에는 0 번째부터 데이터를 두고 비교시 마다 앞에 데이터가
있는지 없는지( 위 소스에서 j 가 -1 이면 더 이상 앞 데이터가 없음)를 검사하는 방법이다.
이미 소트된 데이터에서 하나의 데이터가 입력되는 경우 이상적인 소트 방법이라면
아래와 같은 무작위 데이터에선 삽입정렬을 행할 수 없는 것인가?
6 2 9 8 3 4 7
방법은 ,
아래 정렬된 데이터(데이터가 하나이니 당연히 정렬된 상태)에 2 가 입력될 경우에는 삽입정렬을 행할 수 있을 것이다.
6
결과는 2 6 이 될 것이고, 이 정렬된 데이터에 9 가 입력될 경우 삽입정렬을
행하면 2 6 9 가 될 것이고 ,
이 정렬된 데이터에 8 이 입력될 경우 삽입정열을 행하면 2 6 8 9 가 될 것이고....
////쉘 동작보기 ////
////삽입:쉘 비교////
insertion sort 에서 한 번의 비교로 한 칸씩 뒤로 이동하는 것을 개선하여 ,
거리(distance)를 두어 한 번 비교로 여러칸 이동시키는 방법으로 속도를 개선한 소트
방법이다.
어차피 삽입정렬을 하는데 어떻게 속도를 줄 일수 있을까?
아래 보기에서 쉘 정렬에 대해서 개념을 잡아보자. 물론 이 데이터는 삽입 정령에서 가장 최악의 시간을
보이는 데이터이다.
데이터가 역순으로 소트되어 있는 경우 삽입 정렬을 행할 시
총 몇 번의 비교로 완전히 정렬을 끝낼수 있을까?
7 을 위치시키는데 1 번 , 6 을 위치시키는데 2 번, ...
총= 1 + 2 + 3 + 4 + 5 +6 = 21
총 21 번의 비교가 일어난다.
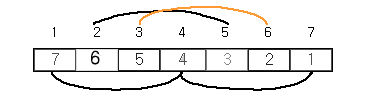
한편 , 거리 3 을 두고 삽입정렬을 한 후, 삽입정렬을 한다면 몇 번의 비교로 정렬을 끝낼수 있을 까?
- 1 번째 , 4 번째 , 7 번째 데이터와 삽입정렬을 한다면
- 2 , 5
- 3 , 6
만약 거리 3 을 주고 삽입 정렬을 한다면
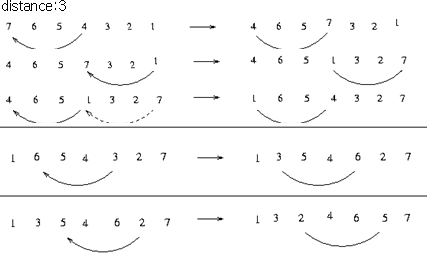
비교 횟수를 계산해 보면
- 간격을 3 을 주고 이 데이터를 만드는데 비교 회수가 5 번 이고
- 삽입정렬을 하는 데 8 번(1 + 2 + 1 + 1 + 2 + 1 ) 으로
총 13 번의 비교로 정렬이 끝난다.
정리하면 ,
insertion sort 에서 한 번의 비교로 한 칸씩 뒤로 이동하는 것을 개선하여 ,
거리(distance)를 두어 한 번 비교로 여러칸 이동시키는 방법으로 속도를 개선한 소트
방법이다.
물론 마지막 과정에서 거리 1 을 주어 insertion sort 가 수행된다.
첫 거리를 얼마나 주면 좋은지 , 간격을 얼마나 줄이면서 마지막에 삽입 정렬로
가는지의 여러가지 연구가 있지만 우리는 간격을 데이터수의 반으로 줄이면서
가는 방법으로 프로그래밍 했다.






