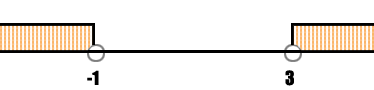차례:
- 집합이란?
- 집합의 종류
-유한 집합
-무한 집합
- 집합의 표현 방법
-원소 나열법
-조건 제시법
- 집합과 집합관계... 집합과 원소 관계
- 집합의 연산
- 합집합
- 교집합
- 차집합
- 여집합
* 드모르간의 법칙 v
- 부분 집합 .. 부분집합의 개수 v
- 합집합의 개수 v
- 포함과 배제의 원리
1. 한 번쯤 집고 넘어가야 할 개념
(1) 부분집합의 개수
원소의 수가 n 가지인 집합 A 의 부분 집합의 개수는 2^n 가지.........
방법 1
원소의 수 가 세 개인 집합 A 에서 ,
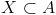 인 X 의 개수는 ?
인 X 의 개수는 ?
A= { 1 , 2 , 3}
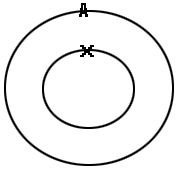 각 원소는 X 안에 들어갈수도 , 들어가지 않을 수도 있다.
그래서 부분 집합의 개수는 2^3 가지...........
각 원소는 X 안에 들어갈수도 , 들어가지 않을 수도 있다.
그래서 부분 집합의 개수는 2^3 가지...........
그러면 A = {1, 2,3,4 } 일 때 아래와 같은 조건으로 B 와 C 를 만들 수 있는 가짓수는 ?
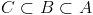
방법 2
(2) 부분집합
(문)집합 A= {1 ,2 ,3} , 집합 A 의 부분 집합의 종류는 ? 이 문제와 동일한 문제로 주머니에
구슬이 세개 있고 , 각 구슬에는 1 , 2 ,3 의 번호가 붙어 있을 때 이 구슬을 꺼내는 경우의 수는?
- 구슬을 뽑지 않는 경우 .. 한가지
- 구슬 하 나를 뽑는 경우 .. 1 , 2 , 3 세가지
- 구슬 두 개를 뽑는 경우 .. 1 2 , 1 3 , 2 3 세가지
- 구슬 세 개를 뽑는 경우 .. 1 2 3 한가지
총 8 가지... 이 는 부분집합의 개수와 동일
(3) 특정 원소를 포함하거나 혹은 포함하지 않는 부분집합의 개수
(4) 드모르간의 법칙
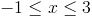
 의 부정은
이렇게 되는 것이 이해가 .........
의 부정은
이렇게 되는 것이 이해가 .........
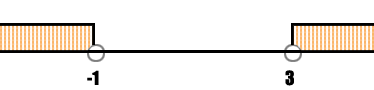
즉 조건식 !( a <=x && x <= b) 는 a > x || x > b 식과 동일한 표현이다.
(4) 포함과 배제의 원리
두 집합의 합집합의 개수를 구할 때 포함과 배제의 원리가 적용된다.
포함과 배제의 원리란 한 번은 더해주고 한 번은 빼 주고...
- 두 집합인 경우... 하나짜리 더해주고 , 두 개짜리 빼주고
- 세 집합인 경우... 하나짜리 더해주고 , 두 개짜리 빼주고 , 세 개짜리 더해주고,
- 네 집합인 경우... 하나짜리 더해주고 , 두 개짜리 빼주고, 세 개짜리 더해주고 , 네개 짜리 빼주고
- ...
이를 직관적으로 이해해 보자......
(4) 정보 연결 문제
출처:
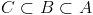
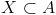 인 X 의 개수는 ?
인 X 의 개수는 ?
 각 원소는 X 안에 들어갈수도 , 들어가지 않을 수도 있다.
그래서 부분 집합의 개수는 2^3 가지...........
각 원소는 X 안에 들어갈수도 , 들어가지 않을 수도 있다.
그래서 부분 집합의 개수는 2^3 가지...........
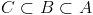
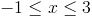
 의 부정은
이렇게 되는 것이 이해가 .........
의 부정은
이렇게 되는 것이 이해가 .........