모든 분수를 소수로 바꾸면 유한 소수 혹은 순환 무한 소수가 된다. 유한 소수란 나누어 가다 떨어지는 소수이고 , 순환 무한 소수란 한 없이 반복되는 소수이다.

유한 소수가 되는 경우는 p,q 가 서로 소인 경우

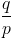
p 가 2 혹은 5 의 인수로만 구성이되면 유한소수가 되고( 분자 분모에 2 혹은 5 를 곱하면 10 을 만들 수 있음) , 그렇지 않으면 순환 무한 소수가 된다.

몇가지 예를 들면 ,

• 1/2 = 0.5 (유한 소수) ... 분모 분자에 5 를 곱하면 5/10 ... 0.5
• 1/3 = 0.333333... (순환 무한 소수) . 순환 마디 3 ... 0.(3)
• 1/4 = 0.25(유한 소수) .. 분모 분자에 5^2 을 곱하면 25/100 .. 0.25
• 1/5 = 0.2 (유한 소수) .분모 분자에 2 를 곱하면 2/10 ... 0.2
• 1/6 = 0.16666... (순환무한 소수) 순환마디 6
• 1/7 = 0.142857142857142857.... (순환무한 소수) 순환마디 142857
• ....

문제는 단위 분수(분자가 1 인 분수)가 주어질 때 이 수의 순환 마디의 크기를 구하는 프로그램을 작성하는 것이다.

입력

출력

입출력 예

입력

3

출력

1

입력

7

출력

6

출처: dovelet