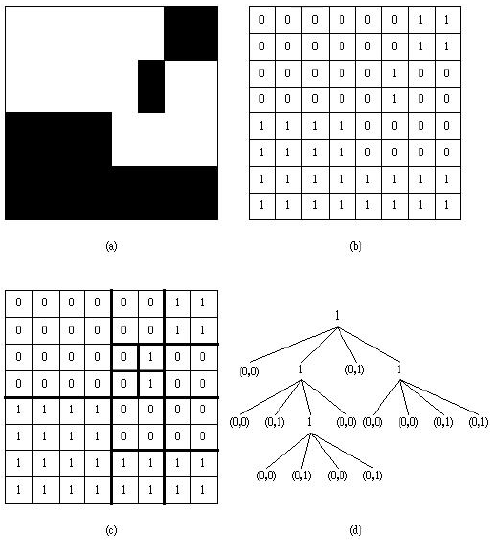

그림 2(b) 는 그림 2(a) 를 나타내는 배열을 나타낸다. 그림 2(b) 의 이진 이미지를 저장하기 위해 일명 쿼드트리 구조를 사용한다.
쿼드 트리는 N*N 배열을 N/2 * N/2 크기로 4 등분 했을 때 모두 같은 값을 가지지 않는다면, 다시 N/2 * N/2 배열에서 같은 이진 값을 가지지 않는다면 다시 .....
이런 식으로 진행하다 4 등분 된 값이 모두 같은 값을 가지면 확장이 종료된다.
그림 2(c) 는 쿼드 트리의 확장이 종료된 후의 배열이 모습이다.
그림 2(a) 에 있는 이진 이미지를 저장하지 않고 , 그림 2(c) 로 부터 엔코드된 그림 2(d) 처럼 쿼드 트리로 이미지를 저장한다.
그림 2(d) 에서 각 노드는 그림 2(c) 에 있는 배열을 나타낸다. 루트노드는 원래 배열을 나타내는 트리에 있는 각 노드의 값이 1 이면 이 때 대응되는 배열의 4 개의 작은 배열로 분할 되는 것을 의미한다.
0 이면 , 노드는 한 쌍의 값을 가진다. 이는 대응되는 배열이 더 이상 분해되지 않는다는 것을 의미 한다. 이 경우 , 두 번째 값은 0 이면 배열에 있는 모든 값이 0 , 1 이면 배열의 모든 값이 1 을 의미한다.
2(a) 의 이진 이미지를 저장하는 대신 그림 2(d) 의 트리를 저장하면 된다.
그림 2(d) 의 트리를 저장하는 방법은 따라오는 그림 2 에 의해서 표현될 수 있다: 이진 이미지 (a) , 이 것의 배열 표현 (b) , 이 것은 쿼드 트리 분할 (c) , 이 것의 쿼드 트리 표현 (d).
code: (1)(0,0)(1)(0,1)(1)(0,0)(0,1)(1)(0,0)(0,0)(0,0)(0,1)(0,1)(0,0)(0,1)(0,0)(0,1).이 코드는 루트에서 리프노드로 그리고 각 레벨에서 왼쪽에서 오른쪽으로 단지 노드의 값의 리스트이다.
괄호와 콤마를 없애면, 이진 수 100101100011000000010100010001 를 얻을 수 있고 , 이것의 16 진 표현은 258C0511 이다.
우리가 해야 할 일은 주어진 이미지에서 대응되는 16 진 값을 구하는 것이다.
입력 2 0 0 0 0 출력 0 입력 4 0 0 1 1 0 0 1 1 1 1 0 0 1 1 0 0 출력 114 입력 8 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 출력 258C0511
출처: Asia Kaohsiung 2003