1. 어떤 수 n 이 소수(prime number)인가?

3453451 이 소수인가?

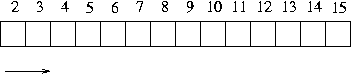
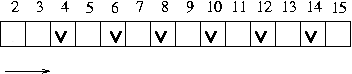
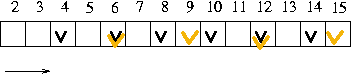
3453451 를 2 로 나누어보고 , 3 으로 나누어 보고 , 4 로 .....

• 3453450 까지 나누어 보는 방법
• 1858 까지 나누어 보는 방법 (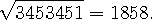xxx )

두 번째 방법이 효율이 좋겠죠.

• 방법1
  소수의 정의에 충실하게 2 부터 n-1 까지 나누어보는 방법.
  ?

  1 2 3 4 5 6 7 8

  for(i = 2;i < n;i++){       if (n%i == 0) break;    }      if (i == n) printf("소수"); // break 에서 반복문을 탈출하면 i 가 n 이 아님.    else printf("소수 아님");   }

• 방법2
  2 부터 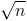까지 나누어보는 방법.
  ?

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  //함수로 bool isprime(int n) {     int i;       for(i = 2; i*i <= n; i++)           if(n%i == 0) return false;       return true; }   //그냥      for(i = 2;i*i <= n;i++){       if (n%i == 0) break;    }      if ( i*i > n ) printf("소수");    else printf("소수 아님"); }

  이게 이해가 쉽지 않죠.

  8 로 예를 들어보면 ,

  • 1 * 8
  • 2 * 4
  • 4 * 2
  • 8 * 1
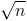  1 * 8 과 2 * 4 를 검사했으면 4 * 2 와 8 * 1 은 다시 중복 검사할 필요가 없겠죠. 그러면 왜 인가? a * b 에서 a <= b 인 규칙으로 수를 선택한다면 중복없이 선택할 수 있습니다. 이 경우 a 와 b 가 같아지는 경계선이 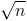입니다.

• 방법3

  방법 2 의 방법에서 짝수 중에 소수는 2 밖에 없으니 미리 걸러 버리는 것입니다.

  ?

  1 2 3 4 5 6 7 8 9 10 11 12

  bool isprime(int n) {     int i;       if(n == 2)  return true;     if(n%2 == 0) return false; // 짝수 중에 2 만 소수임       for(i=3; i*i <= n; i+=2 )           if(n%i == 0) return false;       return true; }

2. 구간에서 소수 판별 법

에라토스테네스의 체(sieve of eratosthenes)

1 에서 1000 사이의 소수를 모두 구하는 문제가 있다고 하면 위의 방법 대로 수 하나씩 하는 것 보다 이 방법이 효율적 입니다.

어떤 수가 소수이면 이 수의 배수는 소수가 될수 없으므로 배수를 모두 없애고 차례대로 하나씩 구하면서 전진하는 방법입니다.

예를 들어, 15 까지의 모든 소수를 구하는 문제를 생각해보면( √15 = 3.xx )

2 는 소수... 2 의 배수 탈락

3 은 소수 ... 3 의 배수 탈락

체크 안된 위치가 소수입니다.

?

1 2 3 4 5 6 7 8 9 10 11

// era[] 배열을 0 으로 클리어   for( i = 2 ; i*i <= 15 ; i++){    if ( era[i] == 0 ){       for( j = i+i ; j <= 15 ; j += i){          era[j] = 1;       }    } }   //era[] 0 이면 소수