두 다항식의 곱 문서

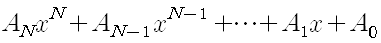
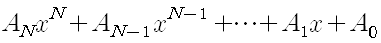
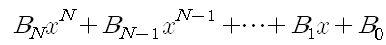
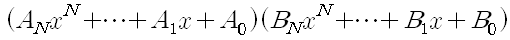을 구할 것이다.

(1) 나이브한 방법

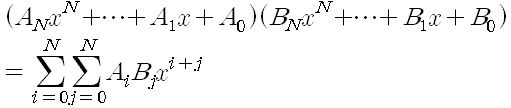
가 되므로 이중for문을 이용하여 O(N^2)의 시간에 답을 구할 수 있다.

하지만 N이 커진다면 위의 방법을 이용하는 것으로는 제 시간 안에 답을 구할 수 없을 것이다. 하지만 위의 방법을 개선하여 O(N^lg3)≒O(N^1.585)의 시간에 답을 구할 수 있도록 Karatsuba algorithm을 응용한 방법이 있다.

(2) Karatsuba algorithm(http://en.wikipedia.org/wiki/Karatsuba_algorithm)

Karatsuba algorithm은 두 수간의 곱을 빠르게 계산하기위해 고안된 방법이다. n자리 B진법의 수 x,y에 대해서 n보다 작은 양의 정수 m을 이용하여

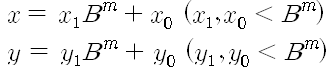
로 나타낼 수 있고, 그 둘의 곱 xy는

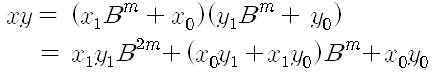
으로 나타난다.

이때

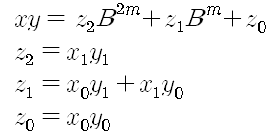
로 나타낼 수 있으며, 특히 z1은

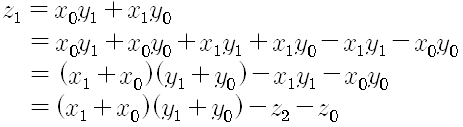
로 나타난다. 이는 큰 두 수의 곱(xy)를 그 보다 절반 작은 수들의 곱 3개(z0,z1,z2)를 이용하여 구할 수 있다는 사실을 의미한다.

위에서 이라고 하고 n자리 수들의 곱을 구할 때 걸리는 연산 횟수를 t(n)이라고 하면

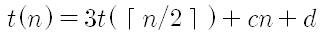
적당한 상수 c, d에 의해(cn+d는 위에서 덧/뺄셈을 해서 생긴 항임.) 가 되어 마스터 정리에 의해

이 된다.

(3) 다항식 계산으로의 응용

Karatsuba algorithm을 이용하여 두 다항식의 곱을 계산하는 것은 거의 같은 과정을 따른다. 위에서의 B를 x라고 생각하는 것이다. 에 대해

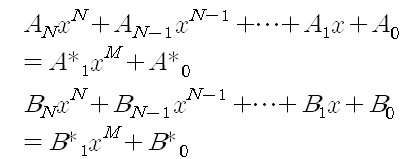
로 M차 미만의 다항식인 을 이용하여 표현할 수 있다.

그리고 위와 마찬가지의 방법을 이용하여

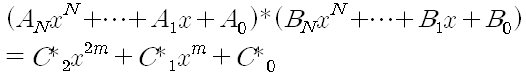
을 만족하는을 구할 수 있다. 따라서 이 방법의 시간 복잡도도 이 된다.

출처:august14