plane sweeping 문서

Plane Sweeping을 이해하기 쉽게 한 가지 문제를 예로 들어 설명하겠습니다.

문제의 개요는 다음과 같습니다. 색종이 여러 장을 한 스크린에 붙이는데, 색종이는 서로 겹칠 수 있습니다. 단, 색종이는 스크린의 가로 세로 방향과 어긋나지 않게 붙여집니다. 색종이의 정보는 스크린의 맨 왼쪽 밑을 (0,0)으로 하고 가로를 X축, 세로를 Y축으로 하여 만들어진 좌표평면 위에서 자신의 왼쪽 밑의 좌표 (A,B) 와 자신의 오른쪽 위의 좌표 (C,D)로 주어집니다. 이 때 이 여러 장의 색종이로 덮혀진 전체 넓이를 구하는 것이 문제입니다.

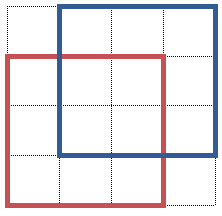
먼저, 4×4 짜리 스크린에 (0,0)-(2,2), (1,1)-(3,3) 색종이를 붙이는 경우를 생각해봅시다.

우리는 손쉽게 색종이가 붙은 전체 면적이 14라는 것을 알 수 있습니다. 하지만 컴퓨터에서 돌린다면 어떻게 될까요? 가장 쉽게 생각할 수 있는 방법은 4×4 이차원 배열을 하나 선언하고 0으로 초기화시킨 후, 색종이를 입력받을 때마다 색종이 안에 포함되는 부분들을 모두 1로 바꾸는 것일 겁니다. 하지만 이것은 매우 느리고 비효율적인 방법입니다.

여기에서 좀 더 속도를 빠르게 해주는 것이 Plane Sweeping입니다. 일단 위의 그림을 봅시다. 빨간 테두리와 파란 테두리에 의해서, 총 다섯 개의 영역으로 나뉘어져 있는 것을 볼 수 있을 것입니다. 만약에 이 다섯 개의 영역에 대해서만 채워져 있다, 아니다를 따지게 된다면 속도는 더 빨라질 것입니다. 하지만 컴퓨터 상에서 ㄱ자, ㄴ자의 도형을 저장하기는 쉽지 않으므로 다음과 같이 영역을 나눕니다.

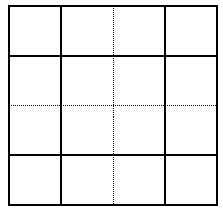
이제 앞서 사용했던 4×4 이차원 배열을 사용하는 방식에서, 3×3 이차원 배열만을 사용해서 표현이 가능해졌습니다. 그런데 이것을 어떻게 알고리즘으로 구현해야할까요?

Plane Sweeping을 위해서는 먼저 다음 과정을 따릅니다.

1. 평면을 자를 값들을 입력 받는다.(A,B)를 입력받으면 X=A, Y=B로 자르게 될 것이고, 이 값들을 배열 두 개에 저장한다. 하나는 X축에 수직하게 자를 선들의 위치, 하나는 Y축에 수직하게 자를 선들의 위치가 된다.단, 중복되는 값이 없도록 체크하도록 한다.
2. 모두 입력받은 후, 두 배열을 각각 오름차순으로 정렬한다.
3. 만약에 어떤 점부터 어떤 점까지를 채우고 싶다면, 위의 1, 2과정에 따라 나온 값들에 따라서 이차원 배열을 채운다.

만약에 그림 들/Pictures 문제와 같은 문제들을 Plane Sweeping을 적용하면서도 위에 서술된 방법보다 더 빠른 방법으로 풀고 싶다면 7 계단에 있는 wireless/wireless ( http://211.229.66.5/30stair/wireless/wireless.php?pname=wireless ) 문제를 꼭 풀어보기 바랍니다.

출처:jhs7jhs