집합 {1,2,3,4,5} 의 순열(permutation) 을 다음과 같이 정의 한다.

P(1) = 4 , P(2) = 1 , p(3)= 5 , ...

그러면 P(P(1)) ? P(P(1)) = P(4) = 2 이다. P(P(3)) 은 3 이다. 그러면 P(P(N)) 은 P(N) 의 순열이다. 보기의 예에서는

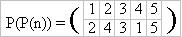
P(P(N)) 을 P2(N) 으로 정의하면 , P(N) = P1(N) , Pk(N) = P( Pk-1(N) ) 이다.

한편, En(N)을 다음과 같이 정의하면( 더 이상 옮길 것이 없는 상태)

그러면 다음 식이 모든 k 에 대해서 성립한다. (EN)k = EN.

본론은 P(N) 을 N 개의 원소를 가지는 순열이라고 약속하면 , 다음 식을 만족하는 자연수 k 가 존재한다.

Pk = EN

또한 Pk = EN 이 되는 가장 작은 자연수 k 를 순열 P 의 차수라 하자.

순열 P 가 주어질 때 차수를 구하는 것이 문제이다.

요약하면 ,

p1: 주어진 순열 

1 2 3 4 5
----------
4 1 5 2 3

p2: 2 번을 접근 후의 순열

1 2 3 4 5
---------
2 4 3 1 5

p3: 3 번을 접근 후의 순열

1 2 3 4 5
---------
1 2 5 4 3

...
pn: n 번 접근 후의 순열 

1 2 3 4 5
---------
1 2 3 4 5

최소  n 을  구하는 게 문제

입력

다음 줄에는 1 .. N 개의 순열이 주어진다. 차례대로 P(1) , P(2) , ...

출력

입출력 예

입력

5
4 1 5 2 3

출력

6

출처:Ural State University Internal Contest October'2000 Junior Session