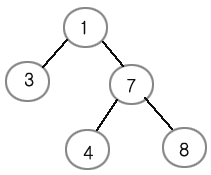
이진 탐색 트리란 숫자들을 노드에 저장해서 탐색에 이용할 수 있게 만든 이진 트리를 말한다.

이 때 언제나 왼쪽 부트리의 숫자들은 부모 노드보다 작고, 오른쪽 부트리의 숫자들은 부모 노드보다 크게 끔 되어 있다. 따라서 찾고자 하는 숫자를 어떤 노드의 숫자와 비교해서 작으면 그 노드의 왼쪽 부트리로,크면 오른쪽 부트리로 계속해서 탐색해 나가다 보면 찾고자 하는 숫자를 발견할 수 있다.

아래 그림과 같은 이진 탐색 트리가 있을 때, 숫자 4 를 찾기 위해서는 루트 노드인 3 부터 시작해서 3 -> 7 -> 4 의 순서로 찾아나서면, 3 번 만에 이 숫자를 찾을 수 있게 된다.

이 문제에서 구하고자 하는 것은,주어진 데이터에 대해서 가장 좋은 구조의 이진 탐색 트리를 구성하는 것이다. 어떤 이진 탐색 트리의 구조가 좋은지는 각 숫자들을 탐색하는데 걸리는 탐색 횟수가 얼마나 적은지로 판단할 수 있다. 이를 위해서 각 숫자마다 이 이진 탐색 트리에서 탐색되는 빈도수가 주어진다.

숫자	1	3	4	7	8
빈도	0.12	0.2	0.47	0.18	0.03

예를들어 위와 같이 빈도가 비율로 주어질 때, 위 그림의 이진 탐색 트리에서는 다음과 같은 식으로 평균 탐색 횟수가 계산된다.

0.12 * 2 + 0.2 * 1 + 0.47 *  3 + 0.18 * 2 + 0.03 * 3 = 2.3

하지만 아래 그림과 같은 구조의 탐색 트리는 더 적은 평균 탐색 횟수를 가지게 된다.

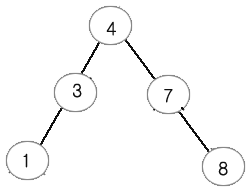
0.12 * 3 + 0.2 * 2 + 0.47 * 1 + 0.18 * 2 + 0.03 * 3 = 1.68

이진 탐색 트리의 구조가 바뀌게 되더라도, 왼쪽 노드부터 오른 쪽 노드까지의 순서는 변하지 않는다는 것에 주의해야 한다. 가장 ㅤ크기가 작은 숫자의 빈도수부터 가장 크기가 큰 숫자의 빈도수까지가 차례대로 주어질 때, 평균 탐색 횟수가 가장 적게 걸리는 이진 탐색 트리의 구조를 출력하는 프로그램을 작성하시오.

입력 형식

첫째 줄은 숫자의 개수 n ( 1 <= n <= 50) 을 나타낸다. 두 번째 줄에는 각 숫자들의 빈도수가 실수로 주어진다. 모든 빈도수의 합은 1 이된다.

출력 형식

평균 탐색 횟수가 가장 적게 걸리는 이진 탐색 트리의 구조를 각 노드의 높이로 출력한다. 왼쪽노드(숫자가 가장 적은 노드)부터 차례대로 높이를 출력하면 된다.

입출력 예

입력

5
0.12 0.2 0.47 0.18 0.03

출력

3 2 1 2 3 

출처:
채점 데이터: