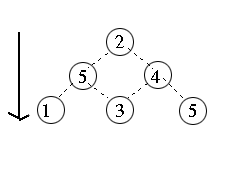
현재 갈수 있는 곳에서 최선을 택하면(greedy method) 2 - 5 - 3(2+5+3=10) 해서 10
하지만 이 방법은 정답이 아니고 2 - 4 - 5(2+4+5=11) 가 정답입니다.
이 문제는 top-down , bottom-up 으로 가능합니다. 이 문서의 목적은 bottom-up 으로의 확장 방식에 대한 이해에 있습니다.
예를 들어 숫자 삼각형이 아래와 같다면
현재 갈수 있는 곳에서 최선을 택하면(greedy method) 2 - 5 - 3(2+5+3=10) 해서 10
하지만 이 방법은 정답이 아니고 2 - 4 - 5(2+4+5=11) 가 정답입니다.
top-down 방식은 확장 방식을 위에서 아래로 확장해 나가는 방식 입니다.
확장 방식은
답은 제일 아래층에서의 최대 값 입니다.
- step1. 제일 위층만 있는 경우 그냥 2 입니다.
- step2. 밑에 층을 포함하는 경우 5 는 2 에서 , 4 도 2 에서 올수 있는 방법 밖에 없으므로 7 , 7 입니다.
- step3. 밑에 층을 포함하는 경우
위층에서 아래 층으로 내려올 때는 2 에서 5 를 선택해야 할지 , 4 를 선택해야할지를 결정할 수 없습니다.
하지만 밑에서 위로 접근하면 결정적으로 선택할 수 있습니다.
과정을 보면 ,
정리하면 ,
입력데이터가 다음과 형식으로 입력된다면,
- 식
- n 층까지 있다면 answ[i][j]는 i 행 j 렬에서 n 행까지 내려가는데 합의 최대
- 답
- ans[1][1]
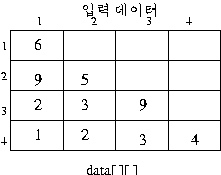
ans[i][j]=data[i][j]+ max( ans[i-1][j] , ans[i-1][j+1])--핵심 소스
for(i=n;i>=1;i--) for(j=1;j>=i;j++) if (ans[i-1][j] > ans[i-1][j+1]) ans[i][j]=data[i][j]+ ans[i-1][j]; else ans[i][j]=data[i][j]+ ans[i-1][j+1];