확장 방법
-
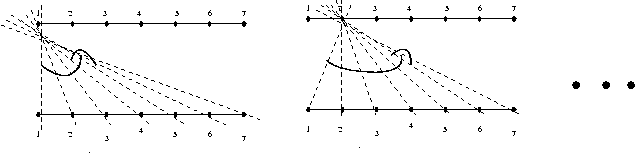
식
-
mns[i,j] 위점 i 에서 아래점 j 까지의 교차하지 않는 다리의 최대수
-
답
- 점의 수가 n 개 이면 mns[n,n]
이 문제는 up-sequence 로 풀이도 가능하나 , 소개하는 방법으로의 풀이는 dp에서 자주 사용(특히 스트링 관련 문제)하는 확장 방법입니다. 이해가 쉽지 않습니다.
확장 방법
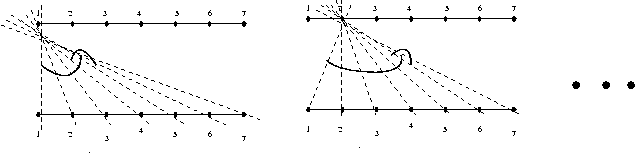
식
mns[i,j] 위점 i 에서 아래점 j 까지의 교차하지 않는 다리의 최대수

답
- 점의 수가 n 개 이면 mns[n,n]
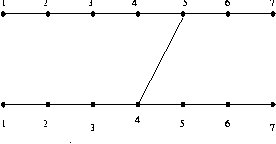
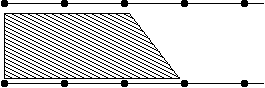
위 점 5 에서 아래 점 4 로 가는 다리가 있을 경우 확장하는 방법에 대해서 알아보면
5,1 5,2 5,3 의 접근 방법은 같다. 그 중 5,3 에 대해서 알아보면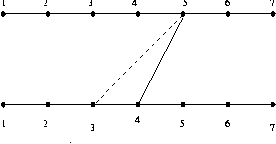
m[5,3] 은 m[4,3] 과 동일하다.(아직 위점 5 번다리에서 연결된 다리를 고려할 필요가 없음)
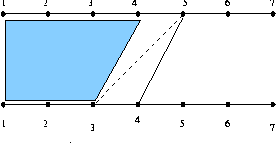
5,4 5,5 5,6 5,7 의 접근 방법은 같다. 그 중 5,6 에 대해서 알아보면
- mns 에 포함되는 경우: m[4][3]+1
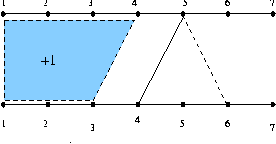
- mns 에 포함되지 않는 경우: m[4,6]
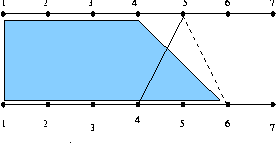
c[i] : 위 점 i 에서 아래 점으로 연결된 아래 점의 번호를 c[i] 라 하자.
---초기화
식: m[1,j]=0 , j < c[1]
1 , j >= c[1]
----처리
식:
m[i,j]= m[i-1,j] , j < c[i]
max(m[i-1,j] , m[i-1,c[i]-1]+1) , j >= c[i]
#include <stdio.h>
int c[]={0,3,4,1,2,5};
int m[6][6];
int main()
{
int i,j;
int max;
//initialize
for(i=1;i < c[1];i++)
m[1][i]=0;
for(i=c[1];i <= 5;i++)
m[1][i]=1;
for(i=2;i <= 5;i++)
for(j=1;j <= 5;j++)
if (j < c[i] ) m[i][j]=m[i-1][j];
else
if( m[i-1][j] > m[i-1][c[i]-1]+1)
m[i][j]=m[i-1][j];
else
m[i][j]=m[i-1][c[i]-1]+1;
//output
for(i=1;i <= 5;i++){
for(j=1;j <= 5;j++){
printf("%3d",m[i][j]);
}
printf("\n");
}
}