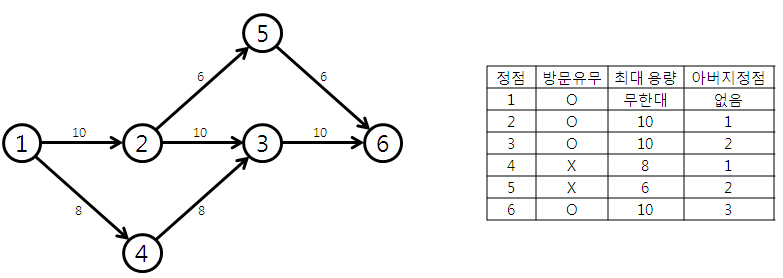
핵심은 직관적인 생각 부분에 나온 것처럼 augument path를 구한 후 해당 용량을 빼주기만 해서는 답을 구하기 전에 path가 끊겨 버리는 경우가 있다는 것입니다. 우선 첫번째 augument path를 구해보겠습니다

10 (1 - 2 - 3 - 6) 이 됩니다. 이번에 흘러간 용량을 전체에서 빼주면 하기 좌측 그림과 같이 되며, 더 이상 augument path가 없으므로 한 번에 흘릴 수 있는 최대 용량은 10이 됩니다. 하지만 실제 한 번에 흘릴 수 있는 최대 용량은 하기 우측 그림과 같이 되어 16이 맞습니다. 16 = 8 ( 1 - 4 - 3 - 6) + 6 (1 - 2 - 5 - 6) + 2 (1 - 2 - 3 - 6)
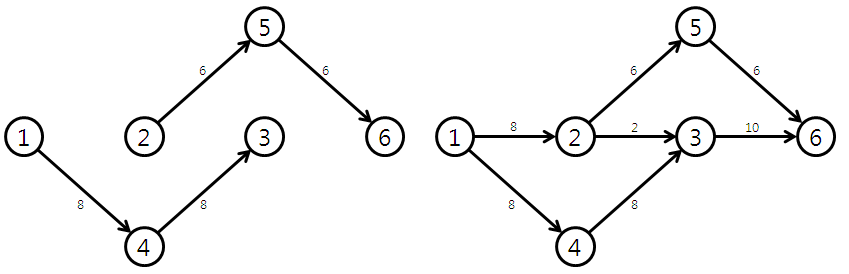
첫번째 augument path 이후에 residual network를 적용한 후 augument path를 다시 구해보겠습니다.
residual network : augument path로 구해진 최대 용량(노드 간 최대 용량이 아님)을 정방향에서 빼주고 역방향에서 더해주면 됩니다
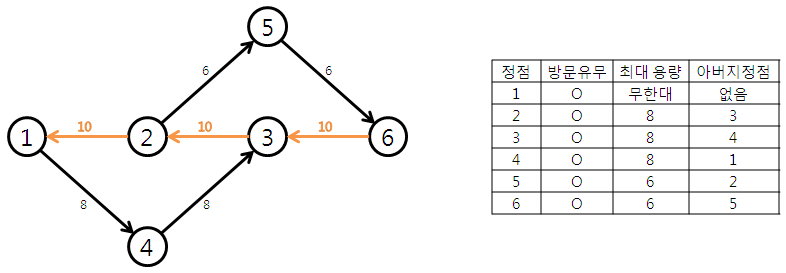
6 (1 - 4 - 3 - 2 - 5 - 6) 이 됩니다. 여기에 residual network를 적용하면 하기와 같이 됩니다. 더 이상 augument path가 없으므로 한 번에 흘릴 수 있는 최대 용량은 16 = 10 + 6 이 됩니다. 거꾸로 간선을 추가한다는 것은 초과된 잉여 용량만큼은 이전 노드로 다시 돌려주고 augument path 한 번 돌때마다 구해진 최대용량만큼만 흘려보내는 것입니다. 쓸데없이 많은 용량을 흘림으로 인해 다른 path를 막아버리는 사태를 막기 위함인 것 같아요.
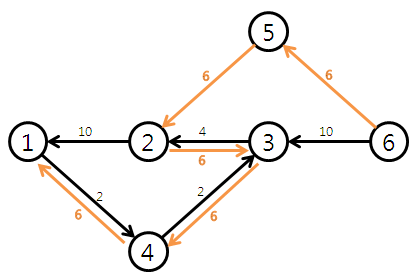
출처:hyowoo