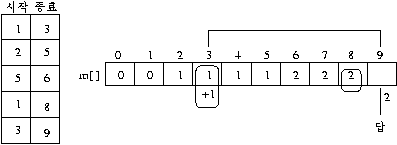
- 종류: 0/1 knapsack 류
- 점화 식:dy[i] : i 시간 까지의 meeting 의 최대 수이고 ,
- 가장 늦은 종료시간이 n 이라면 답은 dy[n].
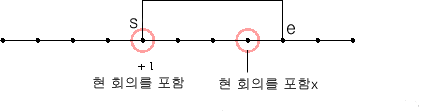
예를 들어 , 시작과 종료시간이 s , e 라면

추가되는 회의를 포함하는 경우 아닌 경우 중 최대
- dy[e - 1] : 회의를 포함시키지 않는 경우
- dy[s] + 1 : 회의를 포함 시킬 경우
두가지 경우 중 최대가 dy[e]
차례대로 과정을 보자.( 그림을 잘못 그려서 m 배열이 dy 배열 ) 풀이를 간단히 하기 위해 미팅 시간은 0 부터 9 까지 입력된다고 가정하자.
- 첫번 째 회의 확장
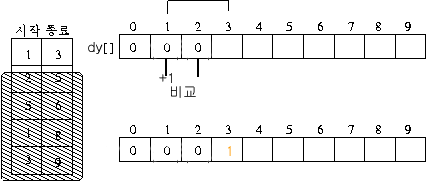
- 작업의 끝이 3 이므로 0 에서 2 까지는 0 으로 채움
- dy[3] = max( dy[3-1] , dy[1] + 1)
- 두번 째 회의 확장
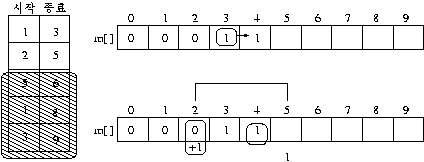
- 세번 째 회의 확장
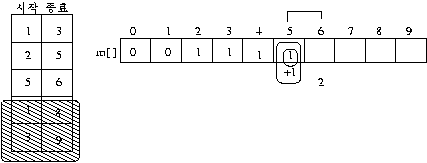
- 네번 째 회의 확장
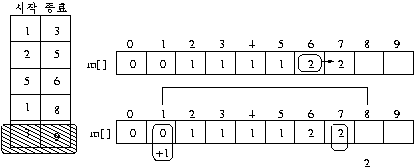
- 다섯번 째 회의 확장