시작 정점(source)에서 목적 정점(sink)까지 한 번에 흘릴 수 있는 최대 용량을 알아내는 문제
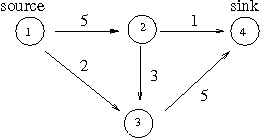
(예시문제) 1 번 정점에서 4 번 정점까지 흘릴 수 있는 최대 용량은? 최대 용량은 6
차례. maximum flow maximum matching minimum cut
먼저 augmenting path 에 대해서 알아보자.augmenting path 문제
시작 정점(source)에서 목적 정점(sink)까지 한 번에 흘릴 수 있는 최대 용량을 알아내는 문제
(예시문제) 1 번 정점에서 4 번 정점까지 흘릴 수 있는 최대 용량은? 최대 용량은 6

이 문제는 언뜻 생각하면 augument path 를 구한 후 해당 용량을 빼 준후 , 다시 augument path 를 구한 후 다시 용량을 빼 주는 동작을 반복하면서 더 이상 소스에서 싱크까지 패스가 존재하지 않을 때 까지 반복하면 될 듯 한데.... 그렇게 해서는 답이 나오지 않는 경우가 발생함
아래 그래프에서
위와 같은 방법으로 하면 최대 플로가 10 .. 하지만 최대 플로는 16
1 에서 2 로 5 가 흐르는 경우 residual network 몇 가지 예를 보면(보기 1) 1 번에서 2 번으로 3 을 흘릴 경우의 residual network 는
51 -------> 23 을 흘린 후 남은 용량은 2 ....거꾸로 3
residual network
21 -------> 2<------3(보기 2) 1 번 정점에서 2 번 정점으로 5 를 흘릴 경우
남은 용량은 없고 거꾸로 5residual network
51 <------ 2
답을 구하는 과정은 augmenting path 를 구한 후 residual network 를 적용...이를 augmenting path 가 0 일 때 까지 반복 . 답은 augmenting path 의 합.
예시 문제에서 최대 플로를 구하는 과정을 살펴 보자.
- step1:
- 먼저 1 에서 4 로 한 번에 흘릴수 있는 augmenting path 는 3 ( 1 - 2 - 3 - 4)
이 패스에 residual network 를 적용하면
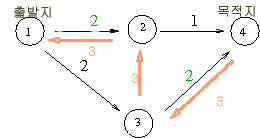
- step2:
- 다시 augmenting path 를 구하면 1 -> 3 ->4 로 2
이 패스에 residual network 을 적용하면
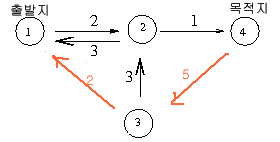
- step3:
- 다시 augmenting path 구하면 1 -> 2 -> 4 로 1
residual network 를 적용
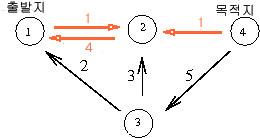
source 에서 sink 로 더 이상의 길이 없으므로(augmenting path가 0)
최대 용량은 3 + 2 + 1 = 6
이렇게 하면 왜 max flow 가 구해지는지 직관적인 이해가 안되네요. 아시는 분 도와 주세요.!!!
출처:dovelet