어떤 섬나라의 해변은 수직 선분과 수평 선분으로만 구성되어 있다. 우리는 이 나라의 해안에 둑을 쌓아 간척지를 만들려고 한다. 이러한 간척지를 만들기 위해서 쌓아야 하는 둑은 수평성분이거나 수직 성분이어야 한다.이때 간척지의 효율은 (간척지의 넓이)/(둑의길이) 로 계산된다.

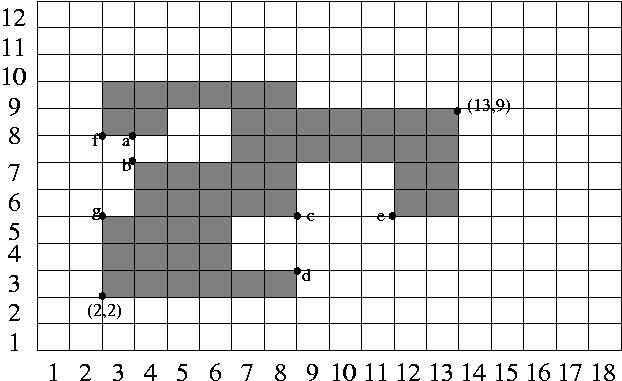
문제는 이 효율을 최대로 하는 간척지를 만들어 주는 둑의 양끝 좌표와 간척지의 넓이를 구하는 것이다.

만일 a-b 지점을 막아서 간척지를 만들면 그로부터 만들어 지는 간척지의 넓이는 5, 둑의 길이는 1 이므로 효율은 5/1 = 5 가된다. 이와 비교해서 f-g 지점을 막으면 둑의 길이는 3, 그로 부터 만들어지는 간척지의 넓이는 8 이므로 효율은 8/3 = 2.667 이 된다.

따라서 a-b 둑이 f-g 둑보다 더 효율적이라고 본다. 계속해서 c-d 지점을 막으면 그 효율은 4/2=2 가 되고 c-e 지점을 막으면 그 효율은 6/3 = 2 가 된다.

따라서 위의 그림과 같은 섬나라에서는 a-b 지점을 막는 것이 가장 효율적인 둑이된다.

입력 형식

• 첫째 줄에는 꼭지점의 개수가 주어진다.
• 두 번째 줄부터는 꼭지점 좌표가 반 시계 방향으로 한 줄에 다섯 개 씩 순서대로 들어 있다.꼭지점의 좌표값은 0 이상 250 이하의 양의 정수이며, 꼭지점의 개수는 100 개 이하이다.

출력 형식

입력과 출력의 예

입력

22
2 2  8 2  8 3  6 3  6 5
8 5  8 7  11 7 11 5 13 5
13 9   8 9  8 10 2 10  2 8
4 8  4 9  6 9  6 7  3 7
3 5  2 5   

출력

5.00

출처:koi 중등부 기출