//작업 중.........

트리의 패스 크기 와 허프만 압축

1.내부 패스(internal path)

트리에서 어떤노드의 패스 크기란?
루트에서 해당 노드까지 오는데 까지의 브랜치 수를 말한다.
예를 들어 , 아래의 그림에서

내부패스 크기(I)=0+1+1+2+2=6

2.외부 패스(external path)

(1) 외부 패스란?

널 링크에 가상의 노드(실패 노드)가 있다고 가정할 때, 이 실패노드까지 오는 경로를 외부 패스라한다.

아래 이진 트리의 외부 패스는

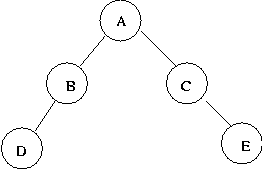
널 링크에 실패노드(사각형 박스)를 붙인 후 , 각 사각형까지의 브랜치수를 합한 것이 외부 패스의 크기가 된다.

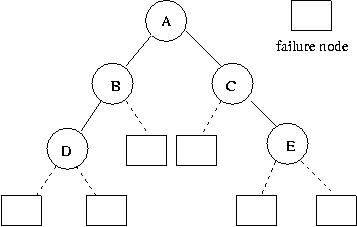
∴ 외부 패스의 크기(E)=3+3+2+2+3+3=16

이진 트리에서 내부 패스의 크기(I)와 외부 패스의 크기(E)는 항상 다음과 같은 성질을 만족한다.

E = I + 2*n

(2) 가중치를 가지는 외부 패스의 크기

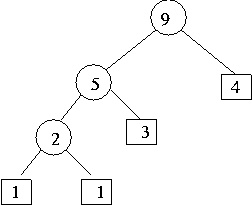
아래 그림과 같이 실패노드에 가중치가 있을 때의 패스의 외부 크기를 알아보자.

E = 4*3 + 3*3 + 2*2 + 1*2 + 1*2 =12 + 9 + 4 + 2 + 2=29

3. huffman code

huffman code 란 외부패스의 크기를 최소로 하는 방법으로 , 가장 작은 데이터 두 개를 선택해서 하나로 합치면서 진행하는 방법(greedy method) (이렇게 하면 최소 외부 패스가 나오는다는 것은 조금 고민해 봐야 할 듯)

(보기) 외부 패스의 크기가 아래와 같을 때 가장 작은 크기의 외부 패스 크기를 구하는 문제이다.

1    1    2    3   4

(풀이)

  1. 1,1,2,3,4 중 작은 데이터 두 개를 하나로 합친다.

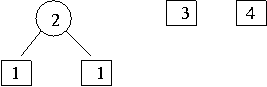
  2. 2 , 3 ,4 중 작은 데이터 두 개를 하나로 합친다.

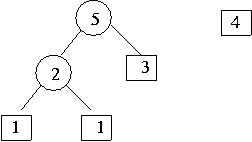
  3. 4 , 5 중 작은 데이터 두 개를 하나로 합친다.

(유제) 다음과 같은 가중치를 가질 때의 최소의 외부 패스 크기는?

1    2    3    4   5
(답) 33

4. 허프만 압축(huffman encoding) 

acaabc

문자열을 압축하려고 한다. 

방법은 각 문자에 이진수를 할당해서 문자열을 압축하려고 한다.

빈도수가 가장 많은 문자에 비트 수를 가능한 짧게 하는게 압축된 사이즈가 줄일 수 있다.

문자 a 가 의 빈도수가 3 
문자 b 의 빈도수가 1
문자 c 의 빈도수가 2

이니 a 에 0 을  b 에 01 을 c 에 1 을 할당 했다고 하자.

그런 후 이 문자열을 압축하면

0100011

자 그리면 

a 가 0
b 가 01
c 가 1

과 압축된 

0100011

로 원래 문자열을 acaabc 를 결정적으로 해독할 수 있는가?


출처:dovelet
[질/답]
[홈으로]  [뒤 로]
[푼 후(0)]