데이터를 압축하는 상대적을 쉬운 방법은 일종의 허프만 트리를 생성해서 할수 있고 그리고 이를 이용해서 압축과 복원을 할수 있다.

대부분의 응용 프로그램에서는 , 이진 허프만 트리가 이용된다. ( 즉 각 노느는 리프 이거나 혹은 2 개의 sub-nodes 를 가진다.

그러나 우리들은 허프만 트리를 구축할 수 있다 서브트리의 임의의 수를 가지고 ( 즉 삼진트리이거나 혹 n-ary 트리)

Z 개의 다른 문자를 포함하는 파일을 위한 허프만 트리는 Z 개의 리프노드를 가진다.

어떤 문자를 표현하는 루트에서 리프로의 패스는 이를 엔코딩해서 결정한다 : 리프노드로의 각 단계는 결정한다

문자를 엔코딩해서 ... 문자는 0 , 1 , 2 ... , N-1 개가 될 수 있다.

빈도수가 많은 문자를 루트에 가깝게 둠으로 , 아닌 문자는 루트에 멀어지게 두어서 원하는 압축을 행 할 수 있다.

엄밀히 이야기 해서 , 그러한 트리는 허프만 트리이다. 결과 엔토딩이 N-ary 결과 파일의 엔코딩 심벌의 최소 수를 테이크 한다면 ...

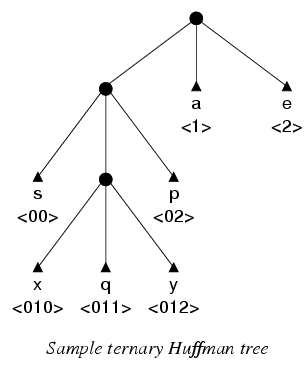
이 문제에서는, 우리는 각 노드가 내부 노드이거나 리프노드이거나 혹은 문자를 엔코드하는 리프 노드이거나 : 문자를 엔코드하지 않는 댕그링 리프은 없다. 그림은 허프만 샘플 허프만 트리를 나타낸다:

a 와 e 문자는 단지 삼진 심볼을 이용해서 엔코드 된다. 자주 나타나지 않는 s 와 p 는 2 개의 삼진 심볼로 엔코드 된다. 아주 빈도수가 적은 심볼 x,q,y 는 3 개의 삼진 심볼을 이용해서 엔코드 된다.

물론 , 우리가 후에 N-ary 심볼의 리스트를 풀기를 원한다면 , 중요하다 아는 것이 ... 어떤 트리가 데이터를 압축하는데 사용한지를 아는게........ 이것은 여러가지 방법으로 이루어 질수 있다. 이 문제는 우리가 다음 방법으로 사용한다: 데이터의 스트림은 앞설 것이다......... 엔코드된 버젼으로 이루어지는 헤드보다 나타나는 Z 문자의 원 파일에

사전 순으로 . 소스 기호 Z 의 수가 주어지고 , 허프만 트리의 airty 라 불리는 값 N 이 주어지고 , 그리고 헤더 , 원본 기호를 엔코드된 심벌로 바꾸는 매핑이 주어진다.

입력

각 테스트 경우에 , 3 개의 라인이 주어진다.

• 파일에 있는 다를 파일의 수 Z ( 2 <= Z <= 20 )
• 허프만 트리의 airty 라 불리는 수 N ( 2 <= N <= 10 )
• 수신된 메시지의 헤드를 나타내는 문자열 ; 각 문자는 0 , (N-1) 의 범위에 있는 숫자이고 이 문자열의 크기는 200 문자보다 작다.

출력

입출력 예

입력

3
3
2
10011
4
2
000111010
19
10
01234678950515253545556575859

출력

0->10
1->0
2->11
0->00
1->011
2->1
3->010
0->0
1->1
2->2
3->3
4->4
5->6
6->7
7->8
8->9
9->50
10->51
11->52
12->53
13->54
14->55
15->56
16->57
17->58
18->59

출처: Northwestern Europe 2002