해시법은 지금까지 설명한 방법과는 전혀 다른 아이디어로 배열을 검색하는 알고리즘으로 잘 실현하면 평균 O(1)의 복잡도(한방에)로 탐색과 삽입 및 삭제를 할 수 있다.
비교에 의해서 검색하는 방법이 아니라 함수식을 이용하여 바로 찾아 가는 검색방법을 말한다.
해시 함수가 2*x + 3 이라면 찾고자 하는 데이터 x 가 3 이라면 2*3+3 즉 9 가 이 데이터의 주소이므로 9 위치를 찾아 가는 방법을 말한다.
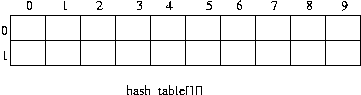
hf(data)=data % 10아래와 같은 해시 테이블이 준비되어 있다고 하자.이 해시 테이블은 20 개의 데이터를 담을 수 있는 테이블이다.
이 테이블에는 10 개의 버킷이 존재하고 , 각 버킷에는 2 개의 데이터를 담을 수 있다. 한 버킷에 담을 수 있는 데이터 수 2 를 슬롯(slot) 이하 한다. 슬롯의 크기는 2 이다.
(풀이)데이터 18 이 온다면 ,
데이터 26,77,192 순으로 입력된다면,
데이터 128 이 입력될 때 , hf(18)=hf(128) 이 된다. 이 때 충돌(collision)이 발생했다고 하고 , 충돌을 발생시키는 18 , 128 을 동의어(synonym)이라 한다. 슬롯이 하나 남아 있으므로 128 을 다른 슬롯에 넣는다.
데이터 38 이 입력된다면 다시 충돌이 발생되고 , 이제 더 이상 빈 슬롯이 없다. 이를 오버플로(overflow)가 발생햇다고 한다.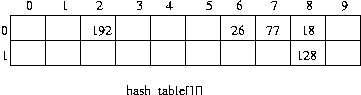
해쉬 주소공간에서 한 기억장소부근에 키기 소복히 모이는 현상을 cluster 가 발생한다고 한다. 이 cluster 발생은 해쉬에서 매우 해로운 현상이다.그래서 해쉬함수를 정할 때 가능한 cluster 를 발행하지 않는 해쉬함수를 정하는 게 중요하다.###
해시를 구현히 고려해야 할 두 가지 사항은
해쉬함수로 많이 사용되는 방법으로는
오버플로의 해결방법으로는
사실상 오버플로의 발생을 완전하게 없애는 것은 불가능하므로 오버플로가 발생했을 시 이를 해결하는 방법이 있어야 한다.
출처:dovelet