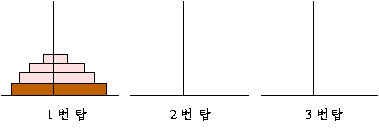
세 개의 탑(1,2,3 번 탑) 있고 첫번 째 탑에 접시가 쌓여져 있다. 단 접시는 작은 접시 위에 큰 접시가 쌓일수는 없다.

1 번 탑에 놓여져 있는 모든 접시를 3 번 탑으로 옮기는 문제이다. 단, 접시는 한 번에 하나씩 옮길 수 있고 , 이동 중간 단계에서도 작은 접시가 큰 접시위 위로 쌓일수는 없다.

입력

출력

입출력 예

입력

3

출력

1 -> 3
1 -> 2
3 -> 2
1 -> 3
2 -> 1
2 -> 3
1 -> 3

설명

처음 이 소스를 보고 어떻게 왜 왜??? 이렇게 될까 ...좌절을 느낀적이 있다. 암튼 재미있지만 조금은 까다로운 듯 하다.

자 그러면 마음을 가다듬고 이제 하노이 재귀 세개로 빠져 봅시다.

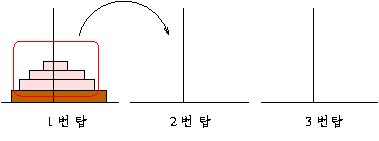
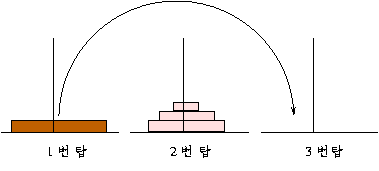
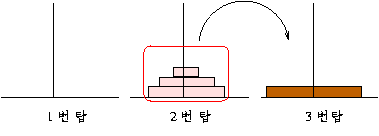
접시 수가 4 개이고, 출발지 탑이 1 번이고 목적지 탑이 3 번 이라면

접시 수	출발 지	임시 저장소	목적지
4	1	2	3

이 문제는

1. 3 개의 접시를 1 번 탑에서 2 번 탑으로

   접시 수	출발 지	임시 저장소	목적지
   3	1	3	2

2. 1 -> 3
3. 3 개의 접시를 2 번 탑에서 3 번 탑으로

   접시 수	출발 지	임시 저장소	목적지
   3	2	1	3

일반화 하면 , 접시 수를 n , 1 번 탑을 x , 2번 탑을 y , 3번 탑을 z 라 하면 ,

접시 수	출발 지	임시 저장소	목적지
n	x	y	z

1. n-1 개의 접시를 출발지 x 에서 목적지 y 로

   접시 수	출발 지	임시 저장소	목적지
   n-1	x	z	y

2. x -> z
3. n-1 개의 접시를 출발지 y 에서 도착지 z 로

   접시 수	출발 지	임시 저장소	목적지
   n-1	y	x	z

//접시수가 3 개일때 소스
#include <stdio.h>

void hanoi(int n,int x,int y,int z)
{

    if (n>0 ){
        hanoi(n-1,x,z,y);
        printf("%d -> %d\n",x,z);
        hanoi(n-1,y,x,z);
    }
}
int main()
{
   hanoi(3,1,2,3);
}