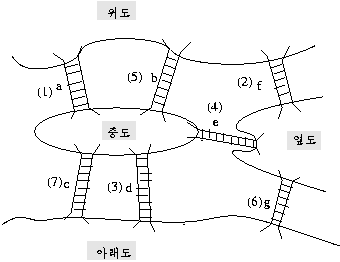
왼쪽 그림은 아래 오른쪽 그림과 같은 형태로 바꾸어 나타낼수 있다.

차례: 그래프 구조 용어 설명 표현그래프 구조는 트리 구조 보다 자유스러운 ( 제약조건이 없는 ) 구조이다.
위도에서 출발하여 모든 다리(koenisberg 다리)를 모두 한 번씩 지나고 자기자리(위도)로 돌아올 수 있는가?그래프구조는 트리보다 제한이 없는 일반적인 용도에 사용할 수 있는 구조이다.

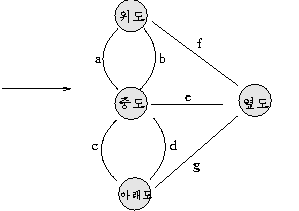
왼쪽 그림은 아래 오른쪽 그림과 같은 형태로 바꾸어 나타낼수 있다.

- 정점(vertex), 간선(edge)
- 섬을 정점 , 다리를 간선이라 한다.
(예) 위의 그래프는 5 개의 정점과 7 개의 간선이 존재한다.
- 무 방향 그래프(undirected graph)
- 간선에 방향이 없는 그래프 즉 왔다리 갔다리 할수 있는 다리 .
(예) 그림 1 은 무 방향 그래프이다.
- 방향성 그래프(directed graph)
- 간선에 방향이 있는 그래프. 이 경우 간선에 화살표를 둔다.
(예)그림 2 는 방향 그래프이다.
- 연결 그래프( connected graph)
- 어떤 정점에서 다른 모든 정점으로 가는 길이 존재하는 그래프를 말한다. 직접가지 않고 돌아가더라도 갈수만 있으면 가능.
그림 1 은 연결 그래프이지만 그림 2 는 연결 그래프가 아니다.
- 완전 그래프(complete graph)
- 어떤 정점에서도 다른 정점모두가 직접 연결된 그래프
(예)완전 그래프가 아니다.( 1 에서 5 로 , 2 에서 3 , ..., 직접 연결된 간선이 없다.)
연결 요소( connected component) - 그래프내에서 연결된 요소. 즉 연결 그래프는 connected component 의 수가 1 개
용어 설명 정점(vertex), 간선(edge) 섬을 정점 , 다리를 간선이라 한다. (예) 5 개의 정점과 7 개의 간선이 존재한다.
무 방향 그래프(undirected graph) 간선에 방향이 없는 그래프 방향성 그래프(directed graph) 간선에 방향이 있는 그래프 연결 그래프( connected graph) 어떤 정점에서도 다른 모든 정점으로 가는 길이 존재하는 그래프를 말한다. 직접가지 않고 돌아가더라도 갈수만 있으면 가능. (예) 연결 그래프이다.
완전 그래프(complete graph) 어떤 정점에서도 다른 정점모두가 직접 연결된 그래프 (예)완전 그래프가 아니다.( 1 에서 5 로 직접 연결된 간선이 없다.)
연결 요소( connected component) 그래프내에서 연결된 요소. 즉 연결 그래프는 connected component 의 수가 1 개 strongly connected graph 방향성 그래프에서 연결 그래프 strongly complete graph 방향성 그래프에서 완전 그래프 차수 (degree) 무 방향성 그래프에서 정점의 차수는 그 정점에 연결된 간선의 수 (예) 1 , 2 번 정점의 차수는 3 , 3 번은 2 , 4 번은 4 , 5 번은 2
진입 차수(indegree) 방향성 그래프에서 정점의 indegree 는 이 정점으로 들어오는 간선의 수 진출 차수(outdegree) 방향성 그래프에서 정점의 outdegree 는 이 정점에서 나가는 간선의 수 경로(path) 그래프상에 간선이 있는 곳을 움직이는 자취 (예)
- 1213 이란 1 번 정점- 2 번정점 - 1 번 정점 - 3 번 정점으로의 패스
- 1251 은 패스가 아님
단순 경로(simple path) 패스중 같은 정점이 없는 패스 (단, 처음과 끝 정점은 같아도 됨) (예) 위 그래프에서
- 12543 (o)
- 125431 (o)
- 1252 (x)
- 12345 (x)
이분 그래프(bipartitle graph) 이분 그래프 G=(V,E) 는 정점들을 두 개의 서로 다른 집합 V1 과 V2=V-V1 로 분할 할 수 있는 무 방향 그래프로 다음과 같은 특성을 갖는다.
- V1 에 속해 있는 어떤 두 정점도 G 에서 인접하지 않음
- V2 에 속해 있는 어떤 두 정점도 G 에서 인접하지 않음
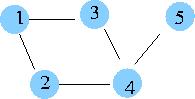
위 그래프는 이분 그래프이다. V1={2,3,5} V2={1,4} 로 나뉘어 질 수 있다.
모든 트리는 이분 그래프이다.
평면 그래프(planar graph) 간선이 서로 교차하지 않는 그래프. 지도로 나타내어지는 그래프는 평면 그래프이다. regular graph 모든 정점의 차수가 같은 그래프 파벌(clique) 무 방향 그래프 G=(V,E) 에서 파벌은 각 정점이 다른 모든 정점에 인접해 있는 부분 그래프이다.
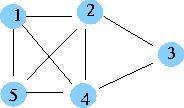
위 그래프에서 {1,2,4} 는 파벌이고 {1,2,3} 은 파벌이 아니다.( 1 과 3 이 연결되지 않음)
최대 파벌(max clique)은 {1,2,4,5} 이다.
multigraph 같은 간선(edge)이 존재하는 그래프

단절 점(articulation point) 그래프 상에 있는 정점 하나 제거시 연결 그래프가 되지 않을시 그 정점을 단절점이라 함.
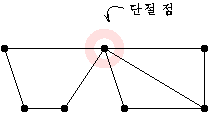
이중 결합 그래프(biconnected graph) 단절점이 존재하지 않는 그래프
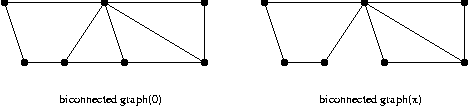
이중 결합 요소(biconnected component) 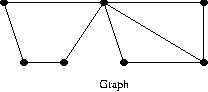
위 그래프의 이중 결합 요소는 아래 그래프의 2 개가 된다.
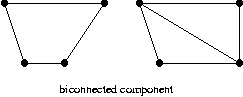
아래 그래프는 이중 결합요소가 아니다. 자체적을 이중 결합되어 있지만 ,이 요소를 완전히 포함하는 이 보다 큰 이중 결합요소가 존재하면 이 그래프는 이중 결합요소가 될 수 없다.
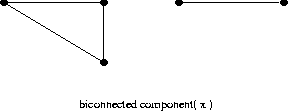
이중 결합 그래프의 이중 결합 요소는 자신 하나만 존재한다.
bridge 간선(edge)을 제거하면 , 그래프가 연결되지 않는 간선을 bridge 함.
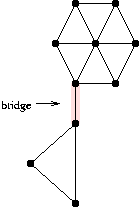
- 오일러 투어(Euler tour) 모든 다리를 한 번 지나고 자기자리로 돌아올수 있는가?
섬(정점)에 연결된 다리(간선)의 수가 짝수
- 오일러 패스(Euler path) 모든 다리를 한 번 지날수 있는가?( 현 위치로 돌아올 필요는 없다)
연결된 다리의수가 홀수인 섬이 두 개이고 다른 섬은 짝수이면 가능
- Hamiltonian cycle 모든 vertex(섬) 를 한 번만 지나고 자기 자리로 돌아 올수 있는가?
(모든 다리를 반드시 사용할 필요는 없다)그림에서는 여러개가 존재 한다.
- a - c - g - f
- a - d - g - f
- ...
- TSP(Traveling Salesperson Problem)--외판원순회 문제

hamiltonian cycle 중에 가장 적은 비용으로 가는 길 찾기 만약 위도에서 시작한다면 a - d - g - f 가 답.