Floyd-Warshall 최단거리 알고리즘

차례
  - 개념 
  - 구현
  - 시간 복잡도

"처음 알고리즘 수업을 들을 때 이 부분 완전히 재미없는 소설 이었습니다. 다이나믹 프로그래밍 뭔지도 모르는 상태에서 들으니.... 지금도 제대로 아는지 모르겠지만 그 때의 심정으로 한 번 ..."

1. 개념

(1) 3 차원으로 개념 잡기

2 차원 보다 3 차원이 생각하기가 쉽습니다. 일단 3 차원으로 개념을 잡고 2 차원으로 넘어갑니다.

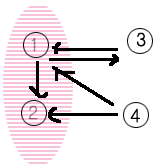
1 .. n 개의 정점(vertex) 을 가지는 그래프에서

• 초기값: m[i][j][0] = w[i][j]
• 점화식 m[i][j][k] 는 i 에서 j 로 가는 데 k 번째 정점까지를 고려한 최단 거리
  • k 번째 정점을 포함하지 않는 경우 : m[i][j][k-1]
  • k 번째 정점을 포함하는 경우 : m[i][k][k-1] + m[k][j][k-1]
  두 가지 중 최소 값
• 해: m[i][j][n]

m[i][j][2]

m[3][5][0]....원래 주어진 데이터

m[3][5][1] ... min( m[3][5][0] , m[3][1][0] + m[1][5][0] )
               3 번 정점에서 5 번 정점으로 가는데 
                  -1 번 정점을 경유하지 않는 경우 
                  -1 번 정점을 경유하는 경우 
                  두 가지중 최소 값.

m[3][5][2] ... min( m[3][5][1] , m[3][2][1] + m[2][5][1] )

m[3][5][3] ... m[3][5][2] 혹은 m[3][3][2] + m[3][5][2] .. m[3][3][2] 가 0 이므로 
               m[3][5][2] 

m[3][5][4] ... min( m[3][5][3] , m[3][4][3] + m[4][5][3])

m[3][5][5] ... m[3][5][4] 혹은 m[3][5][4] + m[5][5][4] .. m[5][5][4] 가 0 이므로
               m[3][5][4] 


m[1][1][1]
  1  2
  1  3
  2  1
  2  2
  2  3
  3  1
  3  2
  3  3

(2) 구현

for(k = 1 ; k <= n; k++)
   for(i = 1 ; i <=n ; i++)
      for(j = 1 ; j <=n ; j++)
         if (m[i][j][k-1] > m[i][k][k-1]+m[k][j][k-1])
            m[i][j][k]=m[i][k][k-1]+m[k][j][k-1];
         else 
            m[i][j][k] = m[i][j][k-1];

(3) 시간 복잡도

dijkstra 방법은 시작점이 주어지고 이 시작점에서 모든 길로의 single source all destination 방법으로 O(n²)이고 floyd-warshall 방법은 모든 정점에서의 최단거리를 구하는 즉 all source all destination 방법으로 O(n³)이다.

dijkstra 방법도 all source all destination 으로 구현하기 위해서는 O(n³)이다.

출처: