차례: 무슨 fix 표현 방법이 무엇인가? 이런 표현 방법이 왜 필요한가 ? 어떻게 연산이 이루어지는가? 이를 어떻게 바꾸나?
- 중위(infix) 표기
- 데이터사이에 연산자가 오는 표기법 , 현재 우리가 사용하는 표기
예를 들어, a + b- 전위(prefix) 표기
- 연산자가 데이터앞에 오는 표기법
+ab- 후위(postfix) 표기
- 연산자가 데이터뒤에 오는 표기법
ab+
a + b * c 란 infix 표현식이 있고 , 이를 컴퓨터로 처리한다고 하면 컴퓨터는 한 문자(보통 token 이란 함)씩 가져와서 연산을 처리하므로 처음 데이터 a , 다음 + , 다음 b 를 가져오는데 여기서 a + b 를 수행할지 아닐지를 뒤에 연산자를 보지 않고는 결정할수 가 없다.이런 고민을 하지않고 결정적 갈수 있고, 또한 괄호도 나타나지 않아 컴퓨터로 계산하기에 적합한 표현이 전위 혹은 후위 표현식이다. 실제적으로 우리가 전위표기식으로 프로그래밍해 놓으면 컴파일러가 전위혹은 후위(주로 후위표현식을 사용)로 바꾼 후 계산을 수행한다.
a + b * c 의 전위와 후위표기식이 다음과 같다고(바꾸는 방법은 뒤에서 기술)하자.
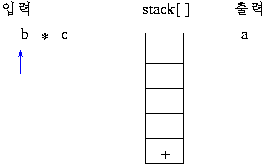
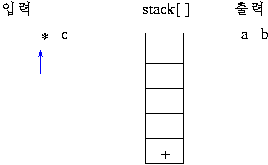
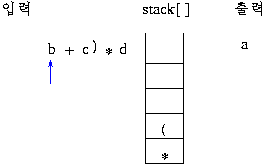
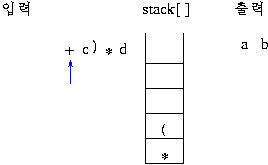
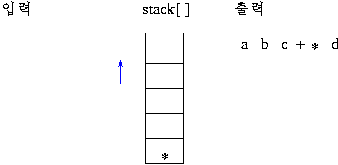
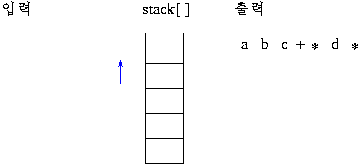
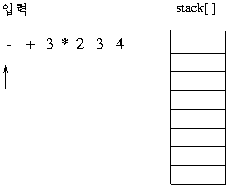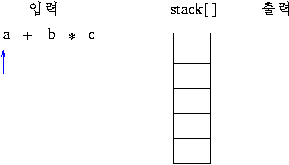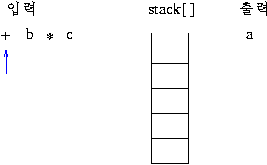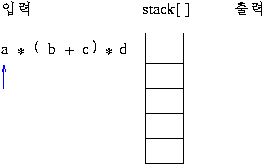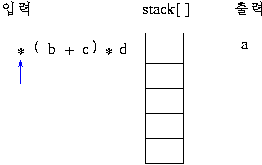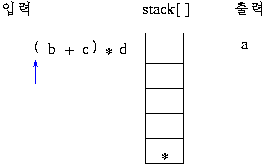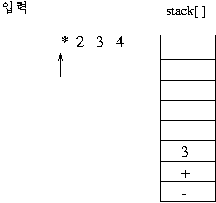
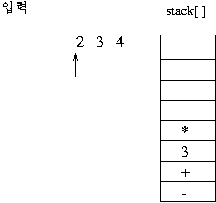
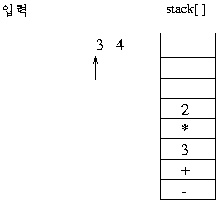
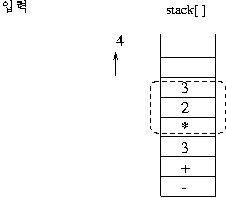
전위 표기: +a*bc 후위 표기: abc*+1)전위 표기식의 연산 과정
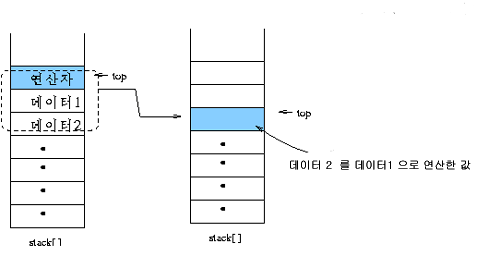
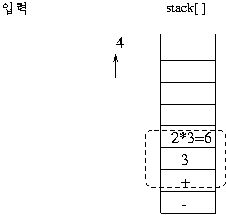
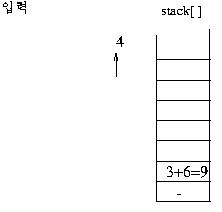
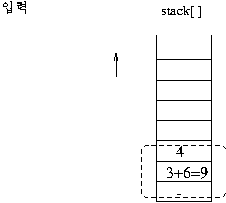
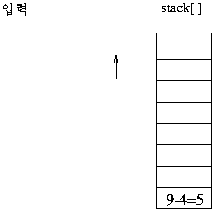
스택의 제일 상위 두 개가 오퍼랜드(데이터)이면 그림과 같이 연산이 이루어 져서 스택에 싸인다.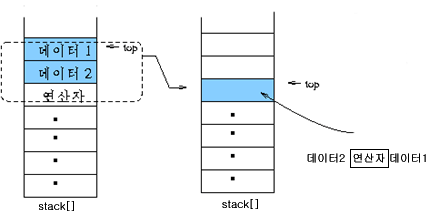
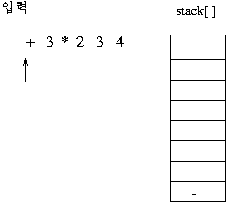
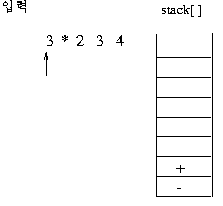
(보기) infix 표현 3 + 2 * 3 - 4 이 prefix 표현으로 연산이 이루어지는 과정을 보자. 이 수식의 전위 표기는
- + 3 * 2 3 4이다.
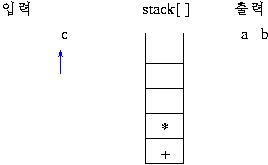
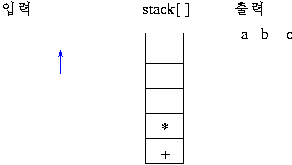
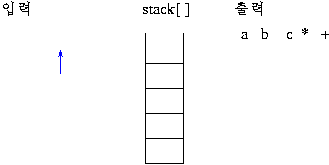
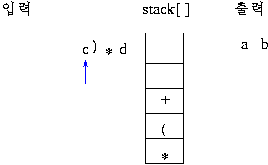
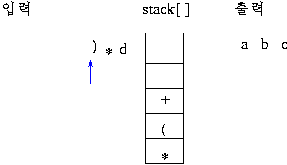
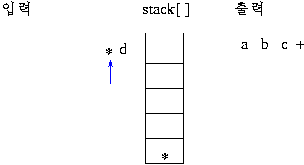
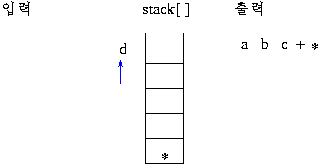
2)후위 표기식의 연산 과정
스택에 연산자가 push 되면 그림과 같이 연산이 이루어져 스택에 싸인다.prefix 는 두 개의 데이터가 스택에서 인접할 때 계산이 이루어지지만(이를 알아내는 것도 부담이 됨) postfix 방법은 연산자가 스택에 push 되는 순간 연산이 이루어지므로 더 쉽게 연산을 할 수 있으므로 prefix 보다는 postfix 방법을 더 선호함. 
1) 괄호가 없는 infix 표현을 postfix 로 변경하는 방법
스택을 이용하여 infix 를 postfix 로 변환하는 방법에 대해서 알아보자.스택에 진입하려는 연산자와 스택의 top 에 있는 연산자의 우선순위를 비교하여 진입하려는 연산자보다 top 에 있는 연산자의 우선순위가 높거나 같으면 연산자를 pop .
연산자 우선순위---
+ , - 는 1 * , / 는 2
스택내에 진입하려는 연산자를 스택내에 위치시킬 때 스택의 top 위치에 있는 연산자보다 우선순위가 커야지만 스택에 위치시킬 수 있다. 다시 말해 스택내에 있는 연산자 중에서 스택으로 들어올려고 하는 연산자보다 우선순위가 높으면 들어올려는 연산자가 클 때까지 pop 한후 , push 해야 한다.괄호가 없으면 연산자가 스택내에 있던 , 스택으로 진입하려고 하던 두 개의 우선순위는 같으나 , 괄호가 있는 수식의 경우에는 ( 가 문제가 된다.
여는괄호 ( 괄호를 만나면 , 다음 토큰으로 닫는 괄호를 만날 때 까지 만난 연산자를 밖으로 꺼내야 하는 동작이 이루어져야 하므로 , 여는 괄호는 스택내에 진입하려고 할 때는 연산의 우선순위가 다른 연산자에 비해 제일 높아야 스택내로 바로 진입이 가능하다. ( 다음 다른 연산자를 만나면 이 연산자는 스택에 진입해야 하는데 , 현재 스택에는 ( 가 있다. 해서 ( 연산자는 스택내에 존재할 때는 다른 연산자에 비해 연산의 우선순위가 제일 낮게 값을 할당해야 한다.
아래 수식의 예를 보자.
(a+b)*(c-d)
( 는 stack 에 push , ) 를 만나면 ( 까지의 내용을 pop 몰론 ( 기호는 출력 하지 않는다.
출처:dovelet
