1.유클리드 호제법

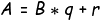
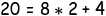
A 를 B 로 나눈 몫을 q , 나머지를 r 이라하면 , ( 20 을 8 로 나눈 몫은 2 나머지는 4)

A , B 의 최대 공약수는 , B , r 의 최대 공약수와 같다. (20 과 8 의 최대공약수는 8 과 4 의 최대 공약수와 같다.)

(1) 직관적으로 이해하기

1. 저는 20 을 생각했습니다.
2. 20 을 두 수의 합으로 표시해 봅니다.

   20 = 8 + 12

   이렇게 하는 순간 20, 8의 공약수와 8,12 의 공약수는 같습니다. 이것이 유클리드 알고리즘의 전부입니다.

   20 , 8 의 공약수 : 1 , 2 , 4 
   8 , 12 의 공약수 : 1 , 2 , 4
   

   우연히 같은 공약수가 나온것 이 아닐까요?

   그러면 20 을 6 + 14 로 나타내면

   20 = 6 + 14

   20 과 6 의 공약수 : 1 , 2
   6 과 14 의 공약수 : 1 , 2
   

30 = 5 + 25 ... 30 과 5 의 공약수 = 5 와 25 의 공약수
9 = 3 + 6 ... 9 와 3 의 공약수 = 3 과 6 의 공약수 
30 = 10 +20 ... 30 과 10 의 공약수 = 10 과 20 의 공약수 
..........
a = b + c
a,b 의 공약수와 b,c 의 공약수는 같다. 
즉 세 수 a,b,c 의 공약수는 같다 이 것이 문제의 핵심이다.

 a , b 의 공약수 k 로 양 변을 나누면 좌편은 0 , 우변 중 b 는  0 이다.
c 도 k 로 나누어져야 등식을 만족한다.


30 과 8 의 최대 공약수를 구하는 과정을 보면 , 

30 = 8 + 22

30 , 8 , 22 의 공약수는 같다.
30 = 8 + 8 + 14  , 8 을 하나 더 분리하더라도 마찬가지 
30 = 8 + 8 + 8 + 6


30 = 8*3 + 6
(30 과  8 공약수)  =( 8 과  6 은 공약수)
같은 공약수를 가지니 최대 공약수도 같다.

(2) 구현

32 와 20 의 최대 공약수를 구하여 보자.

• 32 mod 20 = 12 ... gcd(32,20) = gcd(20,12)
• 20 mod 12 = 8 ... gcd(20,12) = gcd(12,8)
• 12 mod 8 = 4 ... gcd(12,8) = gcd(8,4)
• 8 mod 4 = 0 ... gcd(8,4) = 4

---

• m: 32 n:20
• m: 20 n:12
• m: 12 n:8
• m: 8 n:4
• m: 4 n:0

소스:

   m = 32;
   n = 20;
   for(;;){
      t = m;
      m = n;
      n = t % n;
      if ( n == 0 ) {
        // m 이 최대 공약수 
      }
   }

m < n 인 경우 한 번 루프를 돌면 m > n 상태로 바뀌므로 m 과 n 의 크기에 관계없이 최대 공약수를 구할 수 있다.

2. 최소 공배수(LCM) 구하기

두 수 A,B 의 최대공약수를 G 라하면

A = G * a
B = G * b( a,b 는 서로 소)

두 수의 곱은 A * B = G*L 이다.( L :최소 공배수)

A*B = G*a*G*b = G * G*a*b = G * L

두 수와 최대공약수를 알 때 최소 공배수는 L = A*B/G 로 구할 수 있다.

구현시 A*B 를 먼저하면 자리 넘침이 발생할 수 있으므로 L = A/G*B

3. 확장 유클리드 알고리즘

출처: dovelet