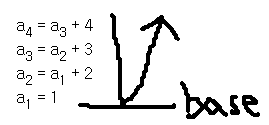
int a(int n)
{
if (n == 1) return 1; //base
return a(n-1) + n; // 재귀
}
int main()
{
printf("%d\n",a(4));
return 0;
}
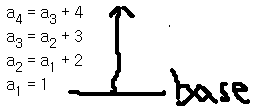
1 , 2 , 3 , 4 , ....이를 식으로 정의하는 방법은 두 가지가 있다.
an = n (n >= 1)
다음으로 귀납적으로 정의하는 방법은 인접한 항과 현재 항과의 관계로 수열의 정의하는 방법이다. 인접한 항이 바로 앞 항일수도 멀리 떨어진 항일수도 있다. 제시된 문제의 경우는 바로 앞 항에 1 을 더하면 현재 항 값을 구할 수 있다.
귀납적으로 정의하는 경우는 처음 시작하는 항(base)을 반드시 밝혀야 유일한 수열이 정의가 된다.
귀납적 정의
그러면 두 가지 중 어떤 방법이 더 나을까? 일반항으로 수열을 정의하는게 더 효율적이다. 왜냐하면 1000 번째 항을 구하는 경우 일반항인 경우 바로 답을 낼 수 있지만 귀납적으로 정의한 경우에는 처음 부터 차례대로 따라가 봐야 한다.
- a1 = 1 (base ... 밑 바닥)
- an = an-1 + 1 (memoization ... 점화식 )
하지만 모든 수열을 일반항으로 표현할 수 없는 경우도 있고 나타낼 수 있더라도 그 방법이 복잡한 경우 차라리 귀납적으로 정의하는게 어떤 수열인지를 더 명확하게 나타낼수가 있다.
유명한 fibonacii 수열은 일반항으로 나타낼수도 있지만 귀납적인 정의가 더 알려져 있다.
이렇게 수열이 귀납적으로 정의된 경우 어떤 항의 값을 컴퓨터를 이용해서 알고자 할 때
가능한 모든 경우를 따지는 방법은 재귀와 동일하지만 답을 구하는 과정이 그림과 같은 차이가 있다.
1
-------------->
답 (재귀함수) 베이스
<-------------
2
답 <------------- (점화식) 베이스
an=an-1 + n에서 a4의 값은 얼마인가?
단 , a1 = 1
(풀이)
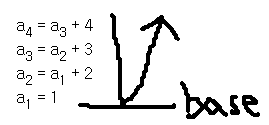
int a(int n)
{
if (n == 1) return 1; //base
return a(n-1) + n; // 재귀
}
int main()
{
printf("%d\n",a(4));
return 0;
}
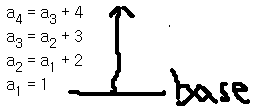
int a[5]; // 다이나믹 방법에서는 전에서 구한 답을 저장하는데 배열을 이용한다.
int main()
{
int i;
a[1]=1; //base
for(i=2;i<5;i++){
a[i]=a[i-1]+i; // 점화식(memoization)--점화식을 구하는게 관건이다.
}
printf("%d\n",a[4]);
return 0;
}
물 좋고 정자좋은 데가 없는 법 이 방법도 배열을 이용해야 하므로 메모리를 많이 차지 하는 태생적 단점이 있지만 재귀보다는 속도면에서는 월등하므로 많이 이용한다.
다이나믹 프로그램은 처음 접할 시에 어려움이 있으므로 몇가지 자주 사용하는 접근 방법으로 다이나믹에 대한 개념을 잡고 여러가지 확장 유형 혹은 나름의 방법을 찾는 방향으로 가자....
출처:dovelet