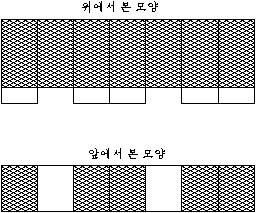
n 개의 같은 크기의 벽장들이 일렬로 붙어져 있고 벽장의 문은 n-2 개만이 있다. 한 벽장 앞에 있는 문은 이웃 벽장 앞에 문이 없다면(즉, 벽장이 열려있다면)그 벽장 앞으로 움직일 수 있다.

그림은 7 개의 벽장의 예이다. 그림에서 2 번 벽장과 5 번 벽장이 열려 있고, 나머지 벽장은 닫혀 있다. 벽장 문은 좌우 어느 쪽이든 그 이웃 벽장이 열려 있다면 그 쪽으로 한 칸 씩 이동할 수 있다. 그림에서는 주어진 상태에서는 1 번 벽장을 닫고 있는 벽장문을 오른 쪽으로 한 칸 이동함으로서 1 번 벽장을 사용할 수 있다. 이때 2 번 벽장은 닫혀져 사용할 수 없다. 역시 5 번 벽장이 열려 있으므로 4 번 벽장 또는 6 번 벽장 앞의 벽장문을 5 번 벽장 앞으로 이동시킬 수 있다.

풀어야 할 문제는 입력으로 주어지는 사용할 벽장의 순서에 따라서 벽장문을 이동하는 순서를 찾는 것이다. 이 때 벽장문의 이동 순서를 최소로 하여야 한다. 입력은 다음과 같이 주어지며, 열려 있는 벽장의 개수는 항상 2 개이다.

예를들어 사용할 벽장순서가 3 1 6 5 이면, 3 번 앞의 문을 2 번으로 옮겨서 3 번 벽장을 사용하고 (문 이동횟수 1), 다음에 1 번과 2 번 앞에 있는 문을 오른 쪽으로 옮겨서( 문 이동횟수 2) 1 번 벽장을 사용하며, 6 번 앞에 있는 문을 왼쪽으로 옮겨서 6 번 벽장을 사용하고( 문 이동횟수 1) , 다시 그 문을 오른쪽으로 옮겨서 5 번 벽장을 사용한다( 문 이동횟수 1). 따라서 문이 이동한 횟수의 합은 5 이다.

또한 같은 벽장을 여러 번 사용할 수 도 있다.

입력 형식

• 첫 번째 줄에 벽장의 개수를 나타내는 2 보다 크고 20 보다 작거나 같은 하나의 정수,
• 두 번째 줄에 초기에 열려 있는 두 개의 벽장을 나타내는 두 개의 정수,
• 세 번째 줄에는 사용할 벽장의 순서의 길이(최대 20), 그리고 그 다음 줄 부터 사용할 벽장의 번호가 한 줄에 하나씩 순서대로 주어진다.

출력 형식

입출력 예

입력

7 
2 5
4
3
1
6
5

출력

5

출처:koi 기출