1 번 정점을 시작 정점으로 하여 모든 정점으로의 최단 경로를 구하는 문제를 생각해보자.
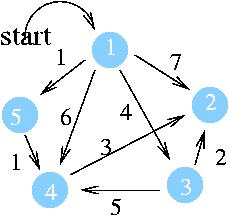
초기 상태
| 정점 |
완료 유무 |
1 번 정점에서 거리 |
아버지 정점 |
| 1 |
완료 |
0 |
0 |
| 2 |
No |
7 |
1 |
| 3 |
No |
4 |
1 |
| 4 |
No |
6 |
1 |
| 5 |
No |
1 |
1 |
단계 1 ---
| 정점 |
완료 유무 |
1 번 정점에서 거리 |
아버지 정점 |
| 1 |
완료 |
0 |
0 |
| 2 |
No |
7 |
1 |
| 3 |
No |
4 |
1 |
| 4 |
No |
6 |
1 |
| 5 |
완료 |
1 |
1 |
1 번 정점에서의 갈수 있는 길 중 최단 경로는 5 번 정점이다.
이 길은 1 번 정점에서 5 번 정점으로의
최단 경로이다.음수가 없다면 돌아서 오는 길이 더 짧은 길이 될 수 없다.
단계 2 ---
| 정점 |
완료 유무 |
1 번 정점에서 거리 |
아버지 정점 |
| 1 |
완료 |
0 |
0 |
| 2 |
No |
7 |
1 |
| 3 |
No |
4 |
1 |
| 4 |
No |
2 |
5 |
| 5 |
완료 |
1 |
1 |
|
| 정점 |
완료 유무 |
1 번 정점에서의 거리 |
아버지 정점 |
| 1 |
완료 |
0 |
0 |
| 2 |
No |
7 |
1 |
| 3 |
No |
4 |
1 |
| 4 |
완료 |
2 |
5 |
| 5 |
완료 |
1 |
1 |
|
5 번 정점에서는 2 3 4 번 정점 중에서 4 번 정점으로 갈수 있고 ,
5 번 정점까지의 크기 (1) + 5 번 정점에서 4 번 정점으로의 길의 크기(1) 이 1 번 정점에서 4 번 정점까지의
크기 6 보다 작기때문에 소스에서의 거리와 아버지 정점을 갱신
완료 정점을 제외한 거리중에서 최소 정점 4 가 선택.
단계 3 ---
| 정점 |
완료 유무 |
1 번 정점에서 거리 |
아버지 정점 |
| 1 |
완료 |
0 |
0 |
| 2 |
No |
5 |
4 |
| 3 |
No |
4 |
1 |
| 4 |
완료 |
2 |
5 |
| 5 |
완료 |
1 |
1 |
|
| 정점 |
완료 유무 |
1 번 정점에서 거리 |
아버지 정점 |
| 1 |
완료 |
0 |
0 |
| 2 |
No |
5 |
4 |
| 3 |
완료 |
4 |
1 |
| 4 |
완료 |
2 |
5 |
| 5 |
완료 |
1 |
1 |
|
4 번 정점에서 2 번 정점으로 가는 길이 5 , 7 보다 더 작으므로 갱신
완료되지 않는 길 중 최소인 정점은 3 번 정점
단계 4 ---
| 정점 |
완료 유무 |
1 번 정점에서 거리 |
아버지 정점 |
| 1 |
완료 |
0 |
0 |
| 2 |
No |
5 |
4 |
| 3 |
완료 |
4 |
1 |
| 4 |
완료 |
2 |
5 |
| 5 |
완료 |
1 |
1 |
|
| 정점 |
완료 유무 |
1 번 정점에서 거리 |
아버지 정점 |
| 1 |
완료 |
0 |
0 |
| 2 |
완료 |
5 |
4 |
| 3 |
완료 |
4 |
1 |
| 4 |
완료 |
2 |
5 |
| 5 |
완료 |
1 |
1 |
|
3 번 정점에서 2 번정점으로 가는 길이 있지만 기존에 있는 길의 크기가 더 작으므로 갱신 되지 않음 .
마지막으로 2 번 정점 선택
소스
#include <stdio.h>
#define MAX 101
int mat[MAX][MAX];
struct n
{
bool visited;
int distant;
int parents;
};
struct n node[MAX];
int main()
{
int n,a,b,m,i,j,min,min_node,p;
//입력
scanf("%d",&n);
while(scanf("%d %d %d",&a,&b,&m) == 3)
mat[a][b] = m;
//초기화
for(i = 1; i <= n; i++){
node[i].visited = false;
node[i].distant = 0x7fffffff;//초기값으로 최대값
node[i].parents = 0;
}
node[1].distant = 0;
//처리
for(p = 1; p <= n; p++){ // n 번 반복 .. 한 번 반복시 마다 최단거리 정점이 하나씩 결정
//최솟값 찾기
min = 0x7fffffff;
for(i = 1; i <= n; i++){
if(node[i].visited == false && min > node[i].distant){
min = node[i].distant;
min_node = i;
}
}
node[min_node].visited = true;
//이 정점을 경유하는 것이 최소이면 갱신
for(i = 1; i <= n; i++){
if(mat[min_node][i] != 0 && node[i].distant>mat[min_node][i]+node[min_node].distant){
node[i].distant = mat[min_node][i]+node[min_node].distant;
node[i].parents = min_node;
}
}
}
//출력
...
return 0;
}
