차례:
-최대값 찾기
-merge sort
-quick sort

작게 해서 정복하고 이 영역을 확장하는 방법.

1. 분할
2. 정복
3. 통합

1. 최대값 찾기

구현

public class Find_Max{
	static int a[8]={6,2,9,8,1,4,17,5};
	
	public static int dc(int low,int high){
		int m, tmp1, tmp2;
		m = (low + high) / 2;
		if(low == high) return a[low];

		tmp1 = dc(low,m);
		tmp2 = dc(m+1,high);
		return (tmp1>tmp2)?tmp1:tmp2;
	}

	public static void main(String[] args){
		int low = 0, high = 7;
		System.out.println(dc(low,high));
	}
}

dc(0,7) ---> tmp1 = dc(0 , 3) --->   tmp1 = dc(0 , 1)  ---> tmp1 = dc(0 , 0)  <=== return a[0] 
                               
                                                      ---> tmp2 = dc(1 , 1) <=== return a[1] 
                                           <============== tmp1 과 tmp2 중 큰 값이 return
                            
                              --->   tmp2 = dc(2 , 3)  ---> tmp1 = dc(2 , 2) <=== return a[2] 

                                                       ---> tmp2 = dc(3 , 3) <=== return a[3] 
                                           <==============  tmp1 과 tmp2 중 큰 값이 return 
                    <=============== tmp1 과 tmp2 중 큰 값이 return  

        ---> tmp2 = dc(4 , 7) --->   tmp1 = dc(4 , 5)  ---> tmp1 = dc(4 , 4) <=== return a[4] 
                               
                                                      ---> tmp2 = dc(5 , 5) <=== return a[5] 
                                           <============== tmp1 과 tmp2 중 큰 값이 return 
                            
                              --->   tmp2 = dc(6 , 7)  ---> tmp1 = dc(6 , 6) <=== return a[6] 

                                                       ---> tmp2 = dc(7 , 7) <=== return a[7] 
                                           <==============  tmp1 과 tmp2 중 큰 값이 return 
                    <=============== tmp1 과 tmp2 중 큰 값이 return  
    <=======최종적으로  tmp1 과 tmp2 중 큰 값이 return 

2. merge sort

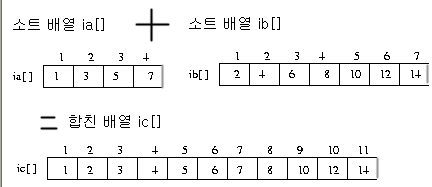
(1) 이미 소트된 배열을 하나로 합치는 방법

(문제) 두개의 정렬 배열 ia,ib 가 주어 질 때 , 이 배열을 합친 배열 ic 를 만드는 것이 문제이다. 물론 ic 배열도 정렬되어 있어야 한다.

구현

변수 세개를 이용한다.

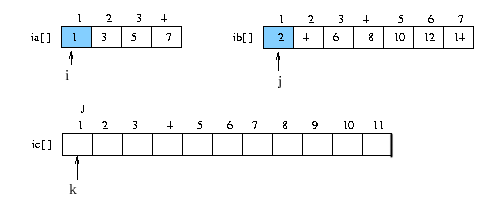
• i , j 가 가르키는 배열 중 작은 내용을 ic 에 쓴 후 i , j 값중 쓴 쪽의 변수 와 k 값을 증가
• 이 과정을 ia[] , ib[] 중 하나라도 끝에 도달할 때 까지 반복

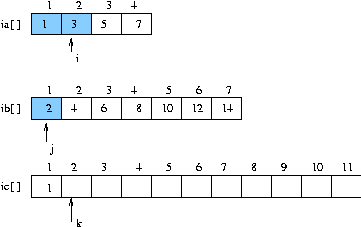
• i 가 가르키는 데이터가 1이고
• j 가 가르키는 데이터가 2 이므로
• 둘 중 작은 값 즉 i 가 가르키는 데이터를 ic 에 쓰고 i 증가 , k 증가

---

(단계 2)

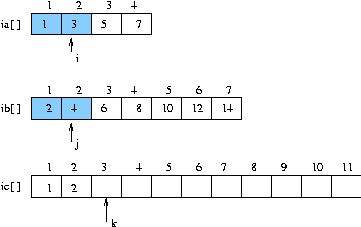
• i 가 가르키는 데이터가 3 이고
• j 가 가르키는 데이터가 2 이므로
• 둘 중 작은 값 즉 j 가 가르키는 데이터를 ic 에 쓰고 j 증가 , k 증가

(단계 3)

• i 가 가르키는 데이터가 3 이고
• j 가 가르키는 데이터가 4 이므로
• 둘 중 작은 값 즉 i 가 가르키는 데이터를 ic 에 쓰고 i 증가 , k 증가

...
...

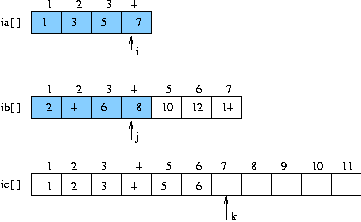
(단계 4)

• i 가 가르키는 데이터가 7 이고
• j 가 가르키는 데이터가 8 이므로
• 둘 중 작은 값 즉 i 가 가르키는 데이터를 ic 에 쓰고 i 증가 , k 증가

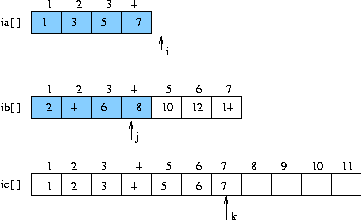
(단계 5)

• 배열 ia[] 에 남은 데이터가 없음.
• 배열 ib[] 는 이미 소트된 상태이므로 , 남은 ib[] 내용을 ic[] 배열로 복사

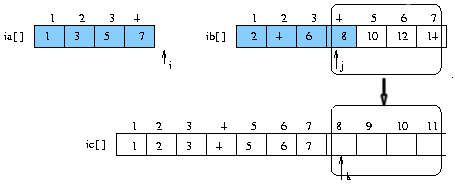
(단계 6)

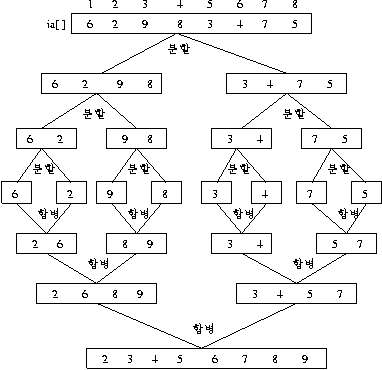
(2) mergesort ( 분할과 정복 )

예를 들어, 8 개의 데이터가 소트되는 과정을 요철로 표현하면

1 에서 8 분할 
  1  4  분할 ,  5 8 분할 
     1  2 분할 , 3 4 분할 
         1 끝 
         2 끝
     1  2 머지 소트
         3 끝
         4 끝
     3  4 머지 소트
  1  4 머지 소트 
     5 6 분할 7 8 분할
         5 끝
         6 끝
     5 6 머지소트
         7 끝
         8 끝
     7 8 머지 소트
  5  8 머지 소트
1  8 머지 소트 

public class Merge_Sort{
	static int s[9] = {0, 6, 2, 9, 8, 3, 4, 7, 5};
	static int u[9];

	public static void merge(int low,int mid,int high){
		int i=low, j=mid+1, k=low;

		while(i <= mid && j <= high){
			if(s[i] < s[j])	u[k] = s[i++];
			else u[k] = s[j++];
			k++;
		}

		if(i > mid)for(i=j;i<=high;i++,k++)u[k]=s[i];
		else for(j=i;j<=mid;j++,k++)u[k]=s[j];
		for(i=low;i<=high;i++)s[i]=u[i];
	}

	public static void sort(int low,int high){
		int mid;
		if(low < high){
			mid=(low+high)/2;
			sort(low,mid);
			sort(mid+1,high);
			merge(low,mid,high);
		}
	}

	public static void output(){
		for(int i=1;i<=8;i++)System.out.print(s[i] + " ");
		System.out.println();
	}

	public static void main(String[] args){
		sort(1,8);
		output();
	}
}

3. quick sort

(1) 왜 quick 인가?

선택 정렬 과 quick 정렬로 왜 이 정렬이 빠른 정렬인지를 알아보자.

두 정렬 방법 모두 한 패스만에 하나의 원소의 자리를 찾는 것은 같다. 하지만 선택정렬은 한 패스에 현재 있는 원소중 가장 작은 데이터 혹은 큰 데이터의 자리를 찾아 옮긴다. 이 것이 왜 빠른가?

다음 7 개의 데이터에서 소트를 하는 과정을 보면서 이해해 보도록 하자.

6 4 9 8 1 2 7

아래 데이터로 선택정렬과 quick 정열을 비교해서 알아보자.

선택 정렬의 한 패스:
1 4 9 8 6 2 7 ... 제일 작은 데이터 1 찾아 6 과 바꾸기 위해서 6 번 비교

quick 정렬의 한 패스:  첫 번째 데이터 6 의 자리를 찾기 위해서 6 번 비교. 

2 1 4              6  8 7 9
-----                 ------
6보다작은데이터       6 보다 큰 데이터  

여기까지는 비교 횟수가 같다. 하지만 다음 패스로 넘어가면 

선택 정렬의 두 번째 패스:




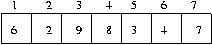
selection sort 의 한 패스 


6 번의 비교 만에 제일 작은 데이터를 제일 처음으로 





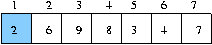
quick sort 의 한 패스 

6 번의 비교 만에 제일 처음 데이터를 정렬




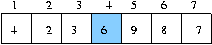
첫 단계에서는 비교회수는 두 방법다 6 번의 비교가 일어난다. 하지만 
선택정렬의 다음 단계에서는 5 번의 비교로 다음 작은 데이터를 2 번째 위치로 옮기지만
quick 정렬은 4 를 소트할 때 4 위의 데이터는 더 이상 비교할 필요가 없므로 2 번의 비교만에
제자리에 놓을 수 있다. 

출처:tncks0121(박수찬)