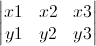
작업 중 입니다. 아직 보지 마세요...

벡터의 외적

(1) 2 차원 평면에서의 외적(활용)

1) 삼각형 면적 구하기

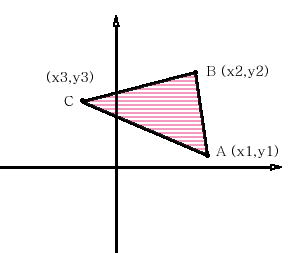
세 점중 임의의 한 점을 선택 합니다. 이 점을 기준으로 반 시계 방향으로 나머지 두 점을 선택 합니다. A 점을 선택했다면 B , C 점 , B 점을 선택했다면 C,A 점 , C 점을 선택 했다면 A,B 점 순으로 선택 합니다.

만약 A 점을 첫 점으로 선택했다면 다음 행렬 식의 값을 구합니다.

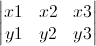
이 행렬식은 \ 방향으로 사선을 그으면서 두 개의 수를 곱 한후 그 합 sum1 이라하면 다음 / 방향으로 두 개씩 곱해서 합을 구한 후 그 합을 sum2 라하면 sum1 에서 sum2 를 빼 주면 됩니다.

• sum1 = x1*y2 + x2*y3 + x3*y1
• sum2 = x2*y1 + x3*y2 + x1*y3
• sum = sum1 - sum2

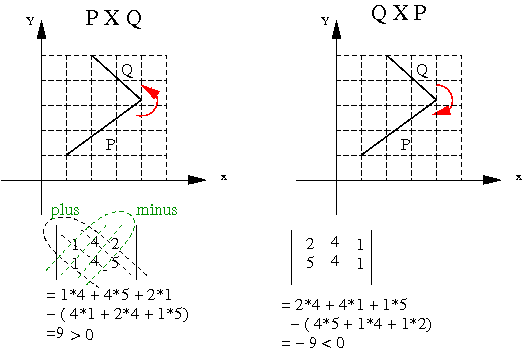삼각형은 세 점이므로 세 점의 행렬식 값을 무작위로 둔 후 음수가 나오면 양수로 바꾸어주어도 가능합니다. 여기에서 반 시계 방향으로 돌리면 양수 , 시계 방향이면 음수가 나오는다는 것을 눈여겨 볼 필요가 있습니다.

2) 시계 방향으로 꺽이는가? 반 시계 방향으로 꺽이는가?

1) 3 차원 입체에서의 외적

1. 한 직선과 이 직선위에 있지 않은 한 점
2. 서로 만나는 두 직선
3. 1 과 같은 말이지만 일직선위에 있지 않은 세 점
4. ...

이 면에 수직인 벡터를 법선 벡터(normal vector)라 하고 이 법선 벡터를 구하는데 외적(cross product)을 사용하고 , 벡터 P , Q 의 외적은 P × Q 로 표시한다.

벡터 P , Q 의 외적 P ×Q

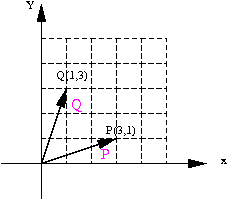
이는 아래와 같이 vector 를 옮겨서 생각해도 동일하다. 그러므로 이제부터 아래 그림처럼 벡터의 종점과 시점을 맞추어서 생각 하도록 하자.

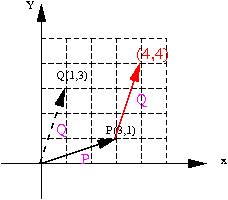
외적의 크기는 두 벡터가 이루는 평행사변형의 크기가 되고,

방향은 기준되는 선분에서 다른 선분으로 오른 주먹을 쥐어서 엄지가 위로 올라가면 양수 , 아래로 내려 가면 음수가 된다. 이 성질이 계산 기학학에서는 약방의 감초처럼 이용되므로 잘 이해하는것이 중요함

P X Q 와 Q X P 는 방향은 반대이고 , 크기는 같다. P X Q 는 P 가 기준이고 , Q X P 는 Q 가 기준 벡터이다.

크기와 방향을 어떻게 구하나?

세점이 이루는 삼각형의 면적을 구하기 위해서는 세 점중 한 점을 기준점으로 해서 시계 반대방향으로 돌리고 , 구해진 값을 평행 사변형의 면적이므로 구한 값의 반이 삼각형의 면적이 된다.

방향을 검사하는 경우는 기준되는 선분의 두 점과 나머지 선분의 종점의 좌표를 위와 같은 방식으로 구해서 양수이면 반시계 , 음수이면 시계 방향이 된다. 값이 0 인 경우 두 선분은 일직선 상에 위치

출처: