볼록 껍질(convex hull)

오른 쪽 볼록 다각형이 왼쪽 점 집합의 볼록 껍질(convex hull)이라 한다.

볼록 껍질은 볼록 다각형이 되어야하고 , 이 점들을 포함하는 사각형 중에 면적을 최소로 햐야 한다. 볼록 껍질의 꼭지점은 점들의 일부이며 꼭지점이 아닌 점들은 볼록 껍질내부에 속하게 된다.

몰론 아래와 같은 그림의 형태가 면적을 더 최소로 하지만 이 다각형는 볼록 다각형이 아니므로 볼록 껍질이 아니다.

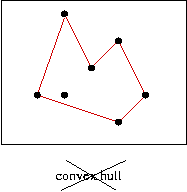
볼록 껍질을 구하는 것은 여러 기하문제의 기본이 되는 중요한 일이다. 최근에 볼록 껍질을 찾는 여러 효율적인 알고리즘이 개발되었다.

여기서는 우선 단순한 방법을 살펴본 후 짐 꾸리기 알고리즘(package wrapping algorithm)과 graham 의 알고리즘을 소개하기로 한다.

convex hull 구하는 방법

• 무작정 방법
• Graham's scan
• Jarvis march

1. 무작정 방법

1) 어떤 선분이 convex hull 의 선분인가 아닌가?

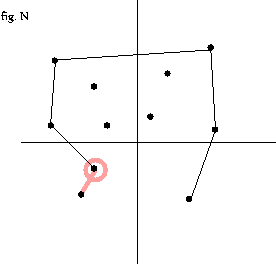
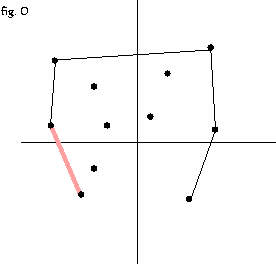
아래 왼쪽 그림의 선분은 convex hull 의 선분이고 오른쪽 그림은 convex hull 의 선분이 아니다.

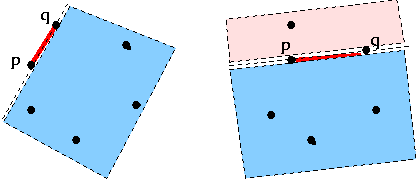
두 점을 이루는 선분이 convex hull 의 선분이 되기 위해서는 이 선분으로 나누어지는 아래/위 영역중 한 영역에만 모든 점이 위치 하면 이 선분은 convex hull 의 선분에 포함된다.

한 선분의 한 영역에 모든 점이 몰려있다는 것을 어떻게 알 수 있을 까? 외적의 성질을 이용한다.

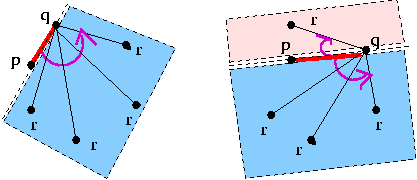
pq 와 qr 외적을 구하여 모두 같은 부호이거나 0 (일직선인 경우) 이면 pq 선분은 convex hull 선분이고 , 하나라도 부호가 다르면 이 선분은 convex hull 에 포함되지 않는 선분이다.

2. Graham scan

1) 각도 순으로 정렬하기

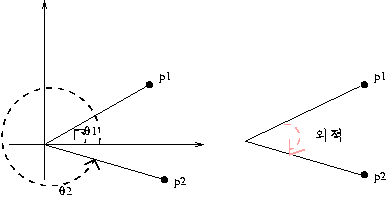
두 개의 점 p1 , p2 가 있을 때 p1 이 이루는 각이 p2 가 이루는 각 보다 더 작다. 어떻게 알 수 있을 까?

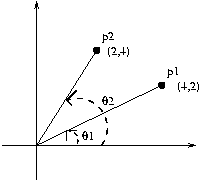
두 점의 기울기를 구한 후 비교로 알수도 있지만 이런 경우에는 두 점이 이루는 상대각도만을 필요하므로 굳이 기울기를 구한후에 대소를 비교할 필요없이 외적을 이용하여 쉽게 구할 수 있다.

p1 과 p2 의 외적을 구하여 반 시계 방향 즉 양수 값이면 p1 이 이루는 각이 더 작고 , 시계 방향 즉 음수값이면 p2 가 이루는 각이 더 작다는 것을 알수 있다.

주의해야 할 것은 아래 그림의 p1 , p2 의 외적을 구하면 시계 방향 즉 음수이지만 p1 이 이루는 각도가 작다. 왜냐하면 외적을 180 도를 기준으로 연산하기 때문이다.

2) extreme point란

주어지는 세점으로 이루어지는 삼각형에 이 점이 포함된다면 이 점은 extreme point 가 될 수 없다. 즉 convex hull 의 꼭지점을 extreme point 라 한다.

아래 그림에서 p 점은 extreme point 가 될 수 없다.

3) Graham's scan 핵심 개념

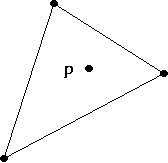
세 점으로 이루어지는 삼각형 내에 어떤 점이 포함되면 이 점은 convex hull 의 꼭지점이 될 수 없다는 성질을 이용한다.

1. 먼저 제일 아래에 있는 점(같은 점이 여러개 이면 가장 오른쪽 점을 선택)을 선택한다. 이점은 반드시 convex hull 에 포함되는 점이다.
2. 이 점을 기준으로 각도 별로 소트를 한다.
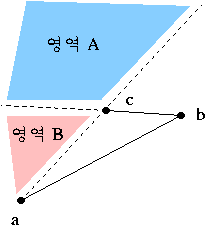
3. 아래 그림과 같이 a b c 로 이루어지는 삼각형에서a 를 기준으로 각도순으로 정렬했다면 다음 점 d 는 영역 A 혹은 영역 B 에 위치할 것이다.

   점 d 가 영역 A 에 위치한다면 점 c 는 convex hull 의 점이 될 수 없다. 왜냐하면 삼각형 abd 의 에 점 c 가 포함될 것이고 , 영역 B 에 점 d 가 위치한다면 이 점을 일단 추가 후 계속 전진한다는 개념이다.

   

   

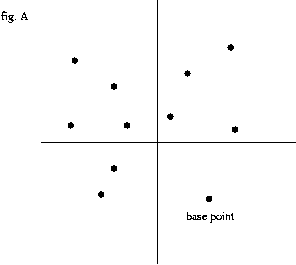
   1. 주어진 점들의 convex hull 을 구하는 문제에서 가장 밑 , 오른쪽 점(base point)을 구한 후 이 점을 기준으로 각도별 정렬(p[1],p[2],p[3],...) --fig. A
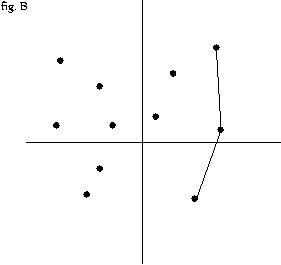
   2. p[1],p[2],p[3] 을 스택에 push (p[1],p[2]가 이루는 간선과 p[2],[3] 와 이루는 간선은 무조건 반시계 방향이므로 )--fig. B
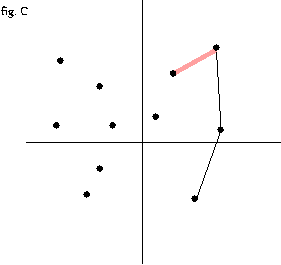
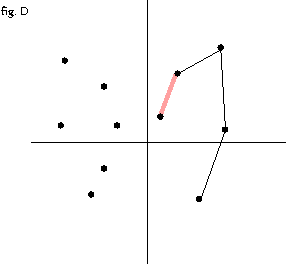
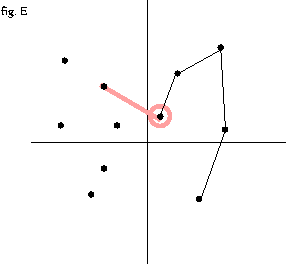
   3. 스택의 stack[top-1],stack[top] 과 stack[top],다음 점 의 외적을 취해서
      • 반시계 방향이면 점을 push
      • 시계 방향이면 pop
      점 이 스택에 push 될 때 까지 반복
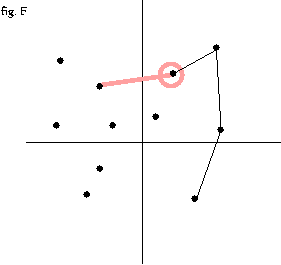
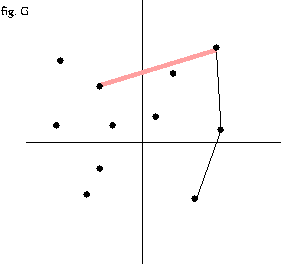
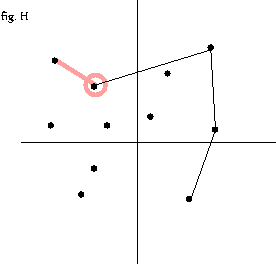
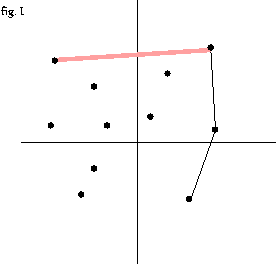
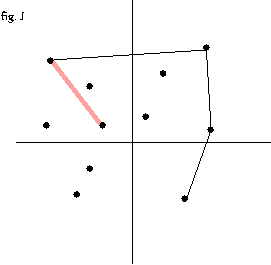
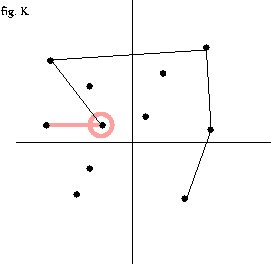
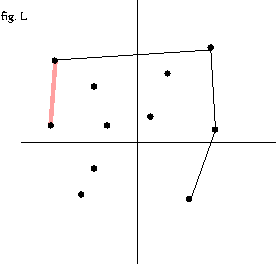
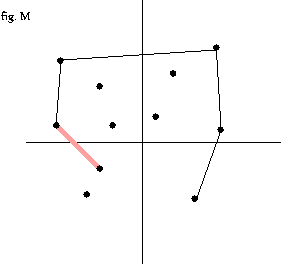
   4. 3 번 과정을 모든 점에 대해서 반복 --fig.C-fig. O
   소스

3. Jarvis march

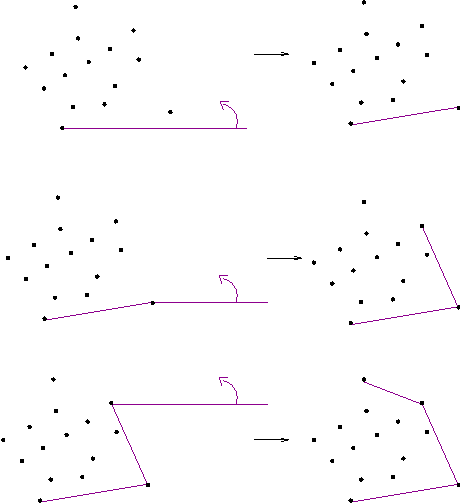
단순하고 , 명확한 방법이다. 개념은 제일 아래 오른쪽 점을 선택 후 이 점에서 고무줄을 줄게 늘여서 위로 올리면 제일 먼저 만나는 점이 convex hull 에 포함되므로 이 를 반복하여 구하는 방법이다.

march up과정

먼저 제일 아래 오른쪽 점을 선택 후

1. 이 점으로 축을 옮긴 후
2. y 값이 양수이거나 0 인 값을 모아서
3. 그 점 중에 외적을 이용하여 가장 각도가 작은 점을 구함
4. 이 점을 원점을 원점으로 놓고 2 -3 번 과정을 반복

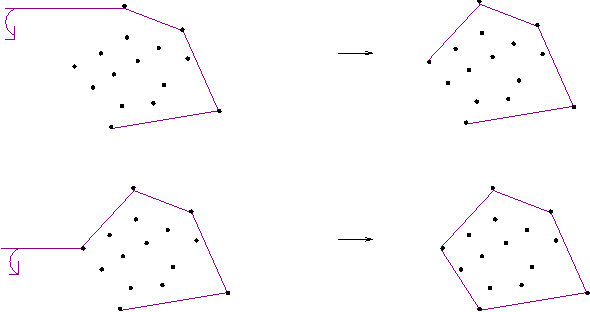
march down과정

1. y 값이 음수이거나 0 인 값을 모아서
2. 그 점 중에 외적을 이용하여 가장 각도가 작은 점을 구함
3. 이 점으로 원점으로 놓고 2 -3 번 과정을 반복

소스

출처: