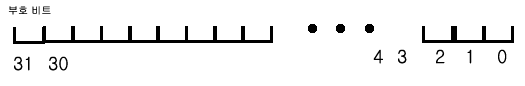먼저 익숙한 10 진수에서 9 의 보수와 10 의 보수에 대해서 알아보자.
(이진수에서도 개념은 동일하다)
(보기) 10 진수 35 의 9 의보수와 10 의 보수는?
(풀이)
10 진수에서 9 의 보수는 9 에서 각 자리를 뺀 값이 9 의 보수가 된다.
35 의 9 의 보수는 64 이다.
(보기) 2 진수 101 의 1 의보수와 2 의보수는?
(풀이)
1 의 보수는 1 을 각 자리에서 빼면 1 의 보수이다.
101 의 1 의 보수는 010 이다. 2 의 보수는 이 수에서 1 을 더한하 011 이 2 의 보수이다. #
정수를 표현하는 방법은 3 가지
설명의 편의를 위해 4 비트로 정수를 표현한다고 가정하자.
- 첫 비트는 부호를 표현한다. 0 은 양수 1 은 음수로 약속
- 나머지 3 비트로 수를 표현한다.
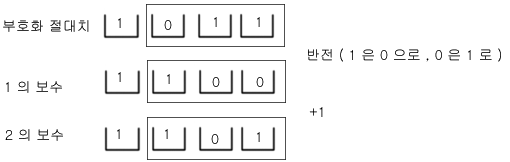
부호화 절대치 방법은 수를 나타내는 자리에 10 진수를 2 진수로 바꾸어 나타내고,
음수이면 첫 비트를 1 , 양수이면 0 로 나타내는 방법이고 ,
1 의 보수 방법 은 구한 부호화 절대치에서 부호 비트가 1 즉 음수인 경우 수 비트를
1 이면 0 으로, 0 이면 1 로 반전(1 을 각자리에서 빼는 것과 동일)하여 나타내는 방법이고
2 의 보수 방법 은 첫 비트가 1 인 음수인 경우 1 의 보수 방법으로 구한 수에 1 을 더하는
방법이다.
(보기) -3 의 부호화 절대치 , 1 의보수 , 2의보수로 표현하면?
(풀이)
기억해야 할 것은 첫 비트 즉 부호 비트는 변하지 않는다는 것이다.
#
정리해보면,
어떤 수를 2 의 보수과정으로 바꿀 때
10 진수를 부호화 절대치로 바꾸고 -->
이를 1 의 보수로 바꾸고 -->
구한 수에서 1 을 더해서 2 의 보수
과정을 거쳐서 구할 수 있다.
문제의 핵심
부호화 절대치에서 1의 보수를 거치지 않고 바로 2 의 보수를 구하는 방법은
부호화 절대치에서 오른쪽에서 왼쪽으로 오다 만다는 첫 비트가 1 일 때 까지 그대로 나머지는
반전(부호 비트 제외) 시키면 구할 수 있다.

이 부분을 이해하면 이 문제에 대한 답이다.
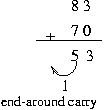
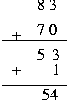
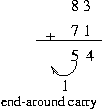 10 의 보수에서는 end-around carry 를 무시한다.
10 의 보수에서는 end-around carry 를 무시한다.