
몇 세기전에 왕 아서와 그의 원탁의 기사는 그들의 우정을 기념하기 위해 매년 새해초에 만나 체스 게임을 한다. 하나의 킹과 다른 위치에서 여러 명의 기사가 존재한다.
아래 체스판은 표준 8 x 8의 체스판이다.

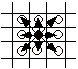
왕은 보드를 벗어나지 않는 한  에서
에서
 로 갈수 있다.
로 갈수 있다.
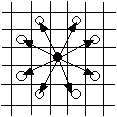
기사는  에서
에서  로 보드를 벗어나지 않는 한
갈수 있다.
로 보드를 벗어나지 않는 한
갈수 있다.
물론 보드 영역 안에서만 이동이 가능하다. 한편, 게이머는 한 칸에 여러 말을 같이 놓을 수 있다. 보드의 한 칸은 충분히 크기 때문에 한 칸에 아무리 많은 말을 동시에 놓아도 문제가 없다고 가정한다.
이 게임의 목표는 가능한 한 적게 말을 움직여 모든 말을 한 자리에다가 두는 것이다. 물론 위의 규칙대로 말을 움직이면서 말이다. 또한, 왕과 하나 이상의 기사가 한 자리에 같이 있게 되면 선수는 왕만 한 칸씩 움직이거나, 기사 중 움직일 것 하나를 골라 왕과 함께 기사가 움직이는 범위로 같이 움직일 수 있다. 기사와 왕을 한꺼번에 움직이는 것은 말을 한 번만 움직인 것으로 친다.
한 장소에 모의기 위한 최소 움직임수를 계산 하는 프로그램을 작성하시오. 물론 어떤 위치에서도 모을 수 있다.
다음 라인에는 왕의 위치가 오고 다음 라인부터 기사들의 위치가 하나이상 온다. 기사들은 없을 수도 보드를 꽉 채울수도 있다. 행의 처음을 1 로 열의 처음을 대문자 A 로 한다.
아래 입력은 왕의 위치가 D4 , 4 명의 기사 위치가 A3 , A8 , H1 , H8 위치에 존재한다는 것이다.
입력 8 8 D 4 A 3 A 8 H 1 H 8 출력 10
위 보기는 They gather at B5. Knight 1: A3 - B5 (1 move) Knight 2: A8 - C7 - B5 (2 moves) Knight 3: H1 - G3 - F5 - D4 (picking up king) - B5 (4 moves) Knight 4: H8 - F7 - D6 - B5 (3 moves) 1 + 2 + 4 + 3 = 10 moves.
출처: ioi 기출